ПРЕОБРАЗОВАНИЕ ДРОБЕЙ

В школе VIII вида учащиеся знакомятся со следующими преоб­разованиями дробей: выражением дроби в более крупных долях (6-й класс), выражением неправильной дроби целым или смешан­ным числом (6-й класс), выражением дробей в одинаковых долях (7-й класс), выражением смешанного числа неправильной дробью (7-й класс).

Выражение неправильной дроби целым или смешанным числом

Изучение данного материала следует начать с задания: взять 2 равных круга и каждый из них разделить на 4 равные доли, подсчи­тать количество четвертых долей (рис. 25). Далее предлагается записать это количество дробью 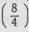. Затем четвертые доли при-

кладываются друг к другу и ученики убеждаются, что получился целый круг. Следовательно,К четырем четвертям добавляет-

ся 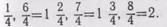последовательно еще по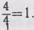 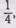и ученики записывают: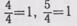

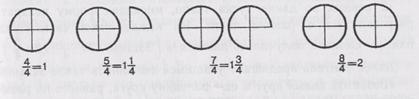
Рис. 25

Учитель обращает внимание учащихся на то, что во всех рас­смотренных случаях они брали неправильную дробь, а в результа­те преобразования получали или целое, или смешанное число, т. е. выражали неправильную дробь целым или смешанным чис­лом. Далее надо стремиться к тому, чтобы учащиеся самостоятель­но определили, каким арифметическим действием это преобразова­ние можно выполнить. Яркими примерами, приводящими к ответу на вопрос, являются: Вывод: чтобы

выразить неправильную дробь целым или смешанным числом, нужно числитель дроби разделить на знаменатель, частное запи­сать целым числом, остаток записать в числитель, а знаменатель оставить тот же. Так как правило громоздкое, совсем не обяза­тельно, чтобы учащиеся заучивали его наизусть. Они должны уметь последовательно рассказать о действиях при выполнении данного преобразования.

Перед тем как познакомить учащихся с выражением непра­вильной дроби целым или смешанным числом, целесообразно по­вторить с ними деление целого числа на целое с остатком.

Закреплению нового для учащихся преобразования способству­ет решение задач жизненно-практического характера, например:

«В вазе лежит девять четвертых долей апельсина. Сколько целых апельсинов можно сложить из этих долей? Сколько четвер­тых долей останется?»

Выражение целого и смешанного числа неправильной дробью

Знакомству учащихся с этим новым преобразованием должно предшествовать решение задач, например:

«2 равных по длине куска ткани, имеющих форму квадрата, разрезали на 4 равные части. Из каждой такой части сшили платок. Сколько получилось платков?».

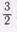Далее учитель предлагает учащимся выполнитьтакое задание: «Возьмите целый круг и еще половину круга, равного по разме­ру первому. Разрежьте целый круг пополам. Сколько всего поло­винполучилось? Запишите: было круга, стало круга.

Таким образом, опираясь на наглядно-практическую основу, рассматриваем еще ряд примеров. В рассматриваемых примерах учащимся предлагается сравнить исходное число (смешанное или целое) и число, которое получилось после преобразования (непра­вильная дробь).

Чтобы познакомить учеников с правилом выражения целого и смешанного числа неправильной дробью, надо привлечь их внима­ние к сравнению знаменателей смешанного числа и неправильной дроби, а также к тому, как получается числитель, например:

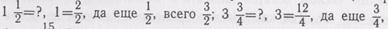всего

будет 15/4. В итоге формулируется правило: чтобы смешанное число выразить неправильной дробью, надо знаменатель умножить на целое число, прибавить к произведению числитель и сумму запи­сать числителем, а знаменатель оставить без изменения.

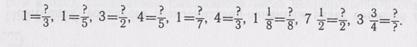
Вначале нужно упражнять учащихся в выражении неправиль­ной дробью единицы, затем любого другого целого числа с указа­нием знаменателя, а уже затем смешанного числа-

Основное свойство дроби¹

Понятие неизменяемости дроби при одновременном увеличении или уменьшении ее членов, т. е. числителя и знаменателя, усваи­вается учащимися школы VIII вида с большим трудом. Это поня­тие необходимо вводить на наглядном и дидактическом материале, причем важно, чтобы учащиеся не только наблюдали за деятель­ностью учителя, но и сами активно работали с дидактическим материалом и на основе наблюдений и практической деятельности приходили к определенным выводам, обобщению.

Например, учитель берет целую репу, делит ее на 2 равные части и спрашивает: «Что получили при делении целой репы пополам? (2 половины.) Покажите репы. Разрежем (разделим) половину репы еще на 2 равные части. Что получим? 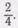Запишем: 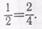Сравним числители и знаменатели этих дробей. Во сколько

раз увеличился числитель? Во сколько раз увеличился знамена­тель? Во сколько раз увеличились и числитель, и знаменатель? Изменилась ли дробь? Почему не изменилась? Какими стали доли: крупнее или мельче? Увеличилось или уменьшилось число долей?»

Затем все учащиеся делят круг на 2 равные части, каждую половину делят еще на 2 равные части, каждую четверть еще на 2 равные части и т. д. и записывают: 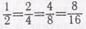и т. д. Потом

устанавливают, во сколько раз увеличился числитель и знамена­тель дроби, изменилась ли дробь. Затем чертят отрезок и делят его последовательно на 3, 6, 12 равных частей и записывают:

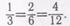
При сравнении дробей обнаруживается, что

числитель и знаменатель дроби увеличивается в одно и то же число раз, дробь от этого не изменяется.

После рассмотрения ряда примеров следует предложить уча­щимся ответить на вопрос: «Изменится ли дробь, если числитель

Некоторые знания по теме «Обыкновенные дроби» исключаются из учебных программ по математике в коррекционных школах VIII вида, но они сообщаются учащимся в школах для детей с задержкой психического развития, в классах выравнивания для детей, испытывающих трудности в обучении математике. В данном учебнике параграфы, где дается методика изучения этого материала, обозначены звездочкой (*).

и знаменатель дроби умножить на одно и то же число (увеличить в одно и то же число раз)?» Кроме того, надо попросить учащихся самим привести примеры.

Аналогичные примеры приводятся при рассмотрении уменьше­ния числителя и знаменателя в одно и то же число раз (числитель и знаменатель делятся на одно то же число). Например, круг делят на 8 равных частей, берут 4 восьмые доли круга,

укрупнив доли, берут четвертые, их будет 2. Укрупнив 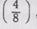доли, берут вторые. Их будет 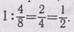Сравнивают последовательно

числители и знаменатели этих дробей, отвечая на вопросы: «Во сколько раз уменьшается числитель и знаменатель? Изменится ли дробь?*.

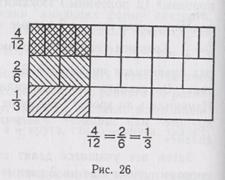
Хорошим пособием являются полосы, разделенные на 12, 6, 3 равные части (рис. 26).

На основании рассмотренных примеров учащиеся могут сде­лать вывод: дробь не изменится, если числитель и знаменатель дроби разделить на одно и то же число (уменьшить в одно и то же число раз). Затем дается обобщенный вывод — основное свойство дроби: дробь не изме­нится, если числитель и знаменатель дроби увеличить или умень­шить в одно и то же число раз.

Сокращение дробей

Предварительно необходимо готовить учащихся к этому преоб­разованию дробей. Как известно, сократить дробь — это значит числитель и знаменатель дроби разделить на одно и то же число. Но делителем должно быть такое число, которое дает в ответе несократимую дробь.

За месяц-полтора до ознакомления учащихся с сокращением дробей проводится подготовительная работа — предлагается из таблицы умножения назвать два ответа, которые делятся на одно и то же число. Например: «Назовите два числа, которые делятся на 4». (Сначала учащиеся смотрят¹ в таблицу, а потом называют эти числа по памяти.) Они называют и числа, и результаты их деления на 4. Затем учитель предлагает ученикам для дроби, 3

например 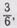подобрать делитель — для числителя и знаменателя (опорой для выполнения такого действия является таблица умно­жения).

Далее учитель предлагает подобрать делитель для дроби (В

какую таблицу надо посмотреть? На какое число можно разделить 5 и 15?) Выясняется, что при делении числителя и знаменателя дроби на одно и то же число величина дроби не изменилась (это можно показать на полоске, отрезке, круге), только стали круп­нее доли:Вид дроби стал проще. Учащиеся подводятся к выводу правиласокращения дробей.

Учащимся школы VIII вида часто оказывается трудно подо­брать наибольшее число, на которое делится и числитель, и знаменатель дроби. Поэтому нередко наблюдаются ошибки такого характера, как 4/12=2/6 т. е. ученик не нашел наибольший общий

делитель для чисел4 и 12. Поэтому на первых порах можно разрешить постепенное деление, т. е. 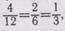но при этом спрашивать, на какое число разделили числитель и знаменатель дроби сначала, на какое число потом и затем на какое число сразу можно было разделить числитель и знаменатель дроби. Такие вопросы помогают учащимся постепенно отыскивать наибольший общий делитель числителя и знаменателя дроби.

Приведение дробей к наименьшему общему знаменателю*

Приведение дробей к наименьшему общему знаменателю нужно рассматривать не как самоцель, а как преобразование, необходимое для сравнения дробей, а затем и для выполнения действий сложения и вычитания дробей с разными знаменателями.

Учащиеся уже знакомы со сравнением дробей с одинаковыми числителями, но разными знаменателями и с одинаковыми знамена­телями, но разными числителями. Однако они еще не умеют сравни­вать дроби с разными числителями и разными знаменателями.

Перед тем как объяснять учащимся смысл нового преобразова­ния, необходимо повторить пройденный материал, выполнив, на­пример, такие задания:

Сравнить дроби 2/5,2/7,2/3 Сказать правило сравнения дробей с

одинаковыми числителями.

Сравнить дроби 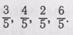Сказать правило сравнения дробей

с одинаковыми знаменателями.

Сравнить дроби 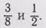Эти дроби учащиеся сравнить затрудня-

ются, так как у них разные числители и разные знаменатели. Чтобы сравнить эти дроби, нужно сделать равными числители или знамена­тели этих дробей. Обычно в одинаковых долях выражают знаменате­ли, т. е. приводят дроби к наименьшему общему знаменателю.

Учащихся необходимо познакомить со способом выражения дробей в одинаковых долях.

Сначала рассматриваются дроби с разными знаменателями, но такие, у которых знаменатель одной дроби делится без остатка на знаменатель другой дроби и, следовательно, может являться и знаменателем другой дроби.

Например, у дробей 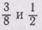знаменателями являются числа 8 и 2.

Чтобы выразить эти дроби в одинаковых долях, учитель предлага­ет меньший знаменатель умножать последовательно на числа 2, 3, 4 и т. д. и делать это до тех пор, пока не получится результат, равный знаменателю первой дроби. Например, 2 умножим на 2, получим 4. Знаменатели опять у двух дробей разные. Далее 2 умножим на 3, получим 6. Число 6 также не подходит. 2 умножим на 4, получим 8. В этом случае знаменатели стали одинаковыми. Чтобы дробь не изменилась, надо и числитель дроби умно­жить на 4 (на основании основного свойства дроби). Получим дробь 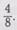Теперь дроби выражены в одинаковых долях. Их

легко и сравнивать, и выполнять с ними действия.

Найти число, на которое нужно умножить меньший знамена­тель одной из дробей, можно делением большего знаменателя на меньший. Например, если 8 разделить на 2, то получим число 4. На это число нужно умножить и знаменатель, и числитель дроби. Значит, чтобы выразить в одинаковых долях несколько дробей, нужно больший знаменатель разделить на меньший, частное умно­жить на знаменатель и числитель дроби с меньшими знаменате­лями. Например, даны дроби 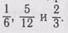Чтобы эти дроби привести

к наименьшему общему знаменателю, нужно 12:6=2, 2x6=12, 306

2x1=2. Дробь 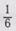примет вид 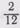. Затем 12:3=4, 4x3=12, 4x2=8. Дробь примет вид 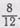Следовательно, дроби примут соответственно вид т. е. окажутся выражен-

ными в одинаковых долях.

Проводятся упражнения, которые позволяют сформировать умения приведения дробей к общему наименьшему знаменателю.

Например, надо выразить в одинаковых долях дроби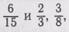

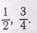
Чтобы учащиеся не забывали то частное, которое получается от деления большего знаменателя на меньший, целесообразно.его

записывать над дробью с меньшим знаменателем. Например, 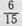и

Затем рассматриваются такие дроби, у которых больший зна­менатель не делится на меньший и, следовательно, не является

общим для данных дробей. Например, Знаменатель 8 не

делится на 6. В этом случае больший знаменатель 8 будем после­довательно умножать на числа числового ряда, начиная с 2, до тех пор, пока не получим число, которое делится без остатка на оба знаменателя 8 и 6. Чтобы дроби остались равными данным, числители нужно соответственно умножить на те же числа. На-

3 5 пример, чтобы дроби тг и •*• были выражены в одинаковых долях,

больший знаменатель 8 умножаем на 2(8x2=16). 16 не делится на 6, значит, 8 умножаем на следующее число 3(8x3=24). 24 делится на 6 и на 8, значит, 24 — общий знаменатель для данных дробей. Но чтобы дроби остались равными, числители их надо увеличить во столько же раз, во сколько раз увеличили знамена­тели, 8 увеличили в 3 раза, значит, и числитель этой дроби 3 увеличим в 3 раза.

Дробь 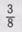примет вид Знаменатель 6 увеличили в 4 раза. Соответственно числитель 5 дроби 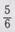надо увеличить в 4 раза. Дроби примут соответственно вид

Таким образом, подводим учащихся к общему выводу (правилу) и знакомим их с алгоритмом выражения дробей в одинаковых долях. Например, даны две дроби ¾ и 5/7

1. Находим наименьший общий знаменатель: 7x2=14, 7x3=21,
7x4=28. 28 делится на 4 и на 7. 28 — наименьший общий знаме­
натель для дробей

2. Находим дополнительные множители: 28:4=7,

28:7=4.

3. Запишем их над дробями: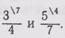

4. Числители дробей умножим на дополнительные множители:
3x7=21, 5x4=20.

Получим дроби с одинаковыми знаменателями .Значит,

дроби мы привели к общему наименьшему знаменателю.

Опыт показывает, что ознакомление учащихся с преобразованием дробей целесообразно проводить перед изучением различных ариф­метических действий с дробями. Например, сокращение дробей или замену неправильной дроби целым или смешанным числом целесооб­разно дать перед изучением сложения и вычитания дробей с одина­ковыми знаменателями, так как в полученной сумме или разности

Придется делать либоодно, либо оба преобразования.

Приведение дроби к наименьшему общему знаменателю лучше изучать с учащимися перед темой «Сложение и вычитание дробей с разными знаменателями», а замену смешанного числа неправильной дробью — перед темой «Умножение и деление дро­бей на целое число».

Сложение и вычитание обыкновенных дробей

1. Сложение и вычитание дробей с одинаковыми знаме­нателями.

Исследование, проведенное Алышевой Т.В.¹, свидетельствует о целесообразности при изучении действий сложения и вычитания обыкновенных дробей с одинаковыми знаменателями использовать аналогию со сложением и вычитанием уже известных учащимся

чисел, полученных в результате измерения величин, и проводить изучение действий дедуктивным методом, т. е. «от общего к част­ному».

Сначала повторяется сложение и вычитание чисел с наимено­ваниями мер стоимости, длины. Например, 8 р. 20 к. ± 4 р. 15 к. При выполнении устного сложения и вычитания нужно склады­вать (вычитать) сначала рубли, а потом копейки.

3 м 45 см ± 2 м 24 см — сначала складываются (вычитаются) метры, а потом сантиметры.

При сложении и вычитании дробей рассматривается общий случай: выполнение этих действий со смешанными дррбями (зна­менатели одинаковые): 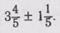В этом случае надо: «Сложить (вычесть) целые числа, затем числители, а знаменатель остается тем же». Это общее правило распространяется на все случаи сложения и вычитания дробей. Постепенно вводятся частные слу­чаи: сложение смешанного числа с дробью, потом смешанного числа с целым. После этого рассматри­ваются более трудные случаивычитания: 1) из смешанного числа дроби: • 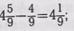2) из смешанного числа целого: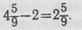

После усвоения этих достаточно простых случаев вычитания учащиеся знакомятся с более трудными случаями, когда требуется преобразование уменьшаемого: вычитание из одной целой едини­цы или из нескольких единиц, например:

В первом случае единицу нужно представить в виде дроби со знаменателем, равным знаменателю вычитаемого. Во втором слу­чае из целого числа берем единицу и также ее записываем в виде неправильной дроби со знаменателем вычитаемого, получаем в уменьшаемом смешанное число. Вычитание выполняется по обще­му правилу.

Наконец рассматривается наиболее трудный случай вычитания: из смешанного числа, причем числитель дробной части меньше числителя в вычитаемом. В этом случае надо уменьшаемое изменить так, чтобы можно было применить общее правило, т. е. в уменьшаемом занять из целого одну единицу и раздробить

в пятые доли, получим 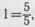да еще , получится 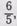пример

примет такой вид:к его решению уже можно применить

общее правило.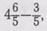

Использование дедуктивного метода обучения сложению и вычи­танию дробей будет способствовать развитию у учащихся умения обобщать, сравнивать, дифференцировать, включать отдельные слу­чаи вычислений в общую систему знаний о действиях с дробями.

Не нашли, что искали? Воспользуйтесь поиском: