Непрерывность функции. Функция называется f(x) называется непрерывной в точке х0, , если она определена в некоторой окрестности этой точки и выполняется равенство

Функция называется f(x) называется непрерывной в точке х₀,, если она определена в некоторой окрестности этой точки и выполняется равенство

,

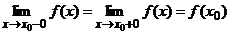где 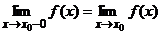, 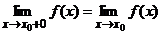односторонние (левый и правый) пределы.

Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0.

Когда у функции f(x) имеются односторонние пределы 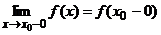и 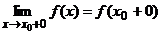и не все числа f(x0), f(x0 - 0) и f(x0 + 0) равны между собой, то разрыв в точке х0 называется разрывом I рода. Величина называется скачком функции.

Если , то разрыв в точке называется устранимым. Здесь полагая получают функцию непрерывную в точке х0.

Если хотя бы один из односторонних пределов не существует или равен бесконечности, то разрыв называется разрывом II рода.

Если функция непрерывна в каждой точке некоторого промежутка, то она называется непрерывной на этом промежутке.

Алгебраическая сумма, произведение и суперпозиция конечного числа непрерывных функций есть функция непрерывная. Отношение двух непрерывных функций есть функция непрерывная, если знаменатель не равен нулю. Отсюда следует, что всякая элементарная функция непрерывна в точках, в которых она определена.

Пример. Исследовать на непрерывность:

1. имеет в точке х=2 разрыв I рода, поскольку 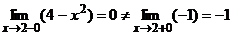. Скачек функции в точке х=2 равен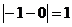

.

2. Функция f(x) = 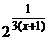не определена в точке х = -1, потому в этой точке она имеет разрыв. Поскольку 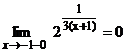и 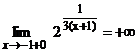, то в точке х = -1 функция имеется разрыв II рода.

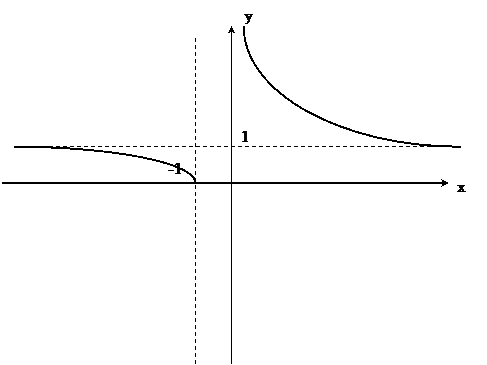Не нашли, что искали? Воспользуйтесь поиском: