Дифференциальное исчисление. Производная. Техника дифференцирования.

Производная. Техника дифференцирования.

Обозначение

Производной функции у = f(x) в точке х0 называется предел или , где = x2 –x1 – приращение аргумента, = у2 – у1 - приращение функции на отрезке [x1, x2]. Функция f(x) называется дифференцированной в точке х, если в этой точке существует производная . Геометрически производная представляет собой угловой коэффициент касательной к графику функции у = f(x) в точке х, т. е. . Если функция дифференцируема в каждой точке промежутка Х, то ее называют дифференцированной на промежутке Х.

Основные правила дифференцирования.

Будем считать, что u=u(x) и v=v(x) – дифференцируемые функции, а С – постоянная. Тогда:

4.

5.

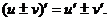
Не нашли, что искали? Воспользуйтесь поиском: