Глава 1. Математический анализ.

Методические указания для практических занятий и самостоятельной работы студентов

По дисциплине Математика

Оглавление

1. Глава 1. Математический анализ………………………3

1.1. Предел функции……………………………………3

1.2. Производная функции……………………………..7

1.3. Производная сложной функции……………..…..10

1.4 Интегральное исчисление………………………...16

1.5 Неопределенный . Его свойства………………17

1.6. Определенный интеграл. Вычисление

площадей плоских фигур……………………………..21

1.7. Метод замены переменной

(метод подстановки)………………………………22

1.8. Дифференциальные уравнения…………………..23

1.9. Однородные дифференциальные

уравнения первого порядка………………………..25

1.10 Частные производные…………………………….27

2. Глава 2. Ряды……………………………………………28

2.1. Числовые ряды……………………………………..28

2.2. Знакопеременные ряды…………………………...31

2.3. Функциональные ряды…………………………….31

3. Глава 3. Основы дискретной математики…………….33

3.1. Множества и отношения………………………….33

4. Глава 4. Основы теории комплексных чисел…………35

4.1. Алгебраическая форма комплексного числа…….35

4.2. Геометрическое представление

комплексных чисел…………………………………….37

4.3. Показательная форма комплексного числа………39

5. Глава 5. Основы теории вероятностей………………….42

5.1. Вероятность. Случайные события…………………42

5.2. Случайная величина. Ее функция распределения..44

5.3. Математическое ожидание и дисперсия

случайной величины………………………………..45

Самостоятельные работы ………………………………..48

Контрольная работа № 1………………………………...57

Глава 1. Математический анализ.

Предел функции.

1. Определение. Таблица замечательных пределов.

Обозначения: множество вещественных чисел.

Опр. 1.1. 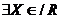, допустим, что каждому значению 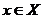по какому – либо закону поставлено в соответствие . Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.

Обозн.

Пример.

Пусть 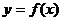определена в некоторой окрестности точки а.

Опр. 1.2. число b называется пределом функци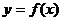и при 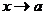, если для любой последовательности аргументов сходящихся к а, соответствующая последовательность значений функций сходится у b.

Обозн.

Таблица пределов:

Свойства пределов:

1) ;

2) ;

3) ;

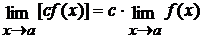4) 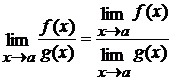(при ).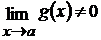

Пример. Вычислить предел.

Задача:

Не нашли, что искали? Воспользуйтесь поиском: