Основной блок. Решение сложных задач на проценты.

Решение задач I типа:

Все задачи этого типа объединяет один способ решения, на основании составленной блок-схемы, вводится неизвестная переменная, которой обозначается все множество, данное в условии; используя процентное соотношение, составляется уравнение.

Задача 1: Участок леса содержит 96% сосен. Лесозаготовительная компания планирует вырубить на этом участке 150 сосен, в результате чего их содержание понизится до 95%. Сколько сосен останется на участке?

Следует обратить внимание на типичную ошибку при решении таких задач. Первоначально, кажется, что 150 сосен – это и есть 1%, который вырубили.

Решение: Составим блок-схему.

- 150 =

х х-150

Опишем задачу:

Пусть х всего деревьев в лесу до вырубки.

Тогда (х-150) деревьев в лесу после вырубки 150 сосен.

Сосен в лесу было 0,96х, а стало 0,95(х-150).

Составим и решим уравнение.

1. 0,96х – 150 = 0,95(х-150)

0,96х – 150 = 0,95х – 0,95∙150

0,96х- 0,95х = 150(1 – 0,95)

0,01х = 150∙0,05 умножим на 100

х = 150∙5

х = 750(деревьев) было в лесу

2. 0,95(750-150)= (сосен) стало в лесу.

Ответ: 570 сосен.

Задача 2: В свежих грибах было 90% воды. Когда их подсушили, то они стали легче на 15 кг при влажности 60%. Сколько было свежих грибов?

Решение. Пусть х кг – свежих грибов, тогда

х кг – 100%

у кг – 90%

у кг = х кг – воды в свежих грибах.

После сушки грибы стали легче на 15 кг, значит, воды в них стало (0,9х-15) кг, что составляет 60%. По условию грибы стали легче на 15 кг, значит, общая масса подсушенных грибов (х-15) кг

(0,9х-15)кг – 60%

(х -15)кг – 100%

(0,9х-15) 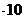= (х-15)

9х -150=6х -90

9х – 6х=-90+150

3х=60

х=60:3

х=20

20 кг – было свежих грибов.

Ответ:20 кг.

Задача 3: Имеется 735 г 16% -ного раствора йода в спирте. Нужно получить 10%-ный раствор йода. Сколько граммов спирта надо долить для этого к уже имеющемуся раствору?

Решение. Найдем массу йода в 16%- нам в растворе:

735 г – 100%

х г – 16%

х= (г) – чистого йода в этом растворе.

Пусть х г – спирта надо долить, тогда общая масса (735+х) г. Масса йода в этом растворе не меняется, но составляет 10%. Составляем пропорцию:

(735+х) г – 100%

117,6 г – 10%

(735+х) = 117,6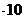

735+х = 1176

х = 1176-735

х = 441

441 г – спирта надо долить для того, чтобы раствор стал 10%-ным.

Ответ:441 г.

Задача 4: В библиотеке книги на английском, французском и немецком языках. Английские книги составляют 36% от всех книг на иностранных языках, книги на французском языке – 75% от книг на английском языке, на немецком языке 185 книг. Сколько книг на иностранных языках в библиотеке?

Решение:

Пусть х книг всего было на иностранных языках, тогда:

(книг) на английском языке;

(книг) на французском; по условию задачи на немецком языке – 185 книг, зная, что всего книг х, составим и решим уравнение:

36х+27х+18500=100х

36х+27х-100х=-18500

63х-100х=-18500

-37х=-18500

х=-18500:-37

х=500

500 книг было всего.

Ответ:500 книг.

Задача 5: В смеси ацетона и воды ацетона в 4 раза меньше, чем воды. Когда к этой смеси добавили 20 литров воды, получили смесь с процентным содержанием ацетона 12%. Сколько литров ацетона было в смеси первоначально?

Решение:

Вся смесь 5х – 100 %

Вода 4х – у %

у =

Ацетона – 20 %

Пусть х литров раствора первоначально, тогда ацетона 20% - 0,2 х литров, После добавления воды, количество ацетона не меняется, но общий вес раствора (х+20) литров. Составим пропорцию:

(х + 20) лит. – 100 %

0,2 х лит. – 12 %

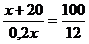
(х+20)12 = 0,2х

12 х+240 = 20х

12 х-20 х = -240

-8 х = -240

х= 30

30 лит. – 100 %

у лит. – 20 %

у = лит.

Ответ: 6 литров ацетона было в растворе первоначально.

Решение задач II типа:

Все задачи этого типа объединяет также один способ решения, на основании составленной блок-схемы, вводятся неизвестные переменные х и у, где х – масса, взятого от первого куска, у – масса, взятого от второго куска. Используя процентное соотношение, составляется система уравнений, в которой первое уравнение выражает содержание одного из данных в условии веществ, входящих в состав слитка (сплава, раствора), а второе – другое вещество.

Составленная блок-схема облегчает понимание условия задачи и способствует правильному решению задачи на проценты.

Все вычисления производятся устно, без использования калькулятора, применяя рациональный (удобный) способ счета.

Задача 1: Имеются два слитка сплава золота и меди. Первый слиток содержит 230 г золота и 20 г меди, второй – 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором 84% золота. Определите массу (г) куска, взятого от первого слитка?

Решение: Составим блок-схему. Числа, указанные зеленым цветом находятся устно, исходя из данных условия задачи.

250 г х у 300 г

250 г х у 300 г

300 г

Определим процентное содержание золота и меди в обоих слитках.

1. 230:250=23:25=0,92=92% - золота в 1 слитке;

2. 100%-92%= 8% - меди в 1 слитке;

3. 240:300=24:30=8:10=0,8=80% - золота во 2 слитке;

4. 100%-80%=20% - меди во 2 слитке.

5. Составим систему уравнений для нахождения переменной х.

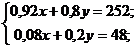умножим второе на (-4),

методом сложения найдем необходимую переменную х.

+

0,6х = 60;

х = 100(г) – масса куска взятого от первого слитка.

Ответ: 100 г.

Задача 2: Три ящика наполнены орехами. Во втором ящике на 10% орехов больше, чем в первом и на 30% больше, чем в третьем. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?

Решение.

1-?, на 80 орехов больше, чем в третьем.

2-?, 10% больше, чем в первом, и на 30% больше, чем в третьем.

3-?

Пусть х – орехов было в первом ящике, z – орехов во втором ящике:

х – 100%

z – 110%

z=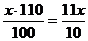

Пусть у орехов было в третьем ящике.

у – 100%

z – 130%

z =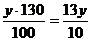

По условию в первом на 80 орехов больше, чем в третьем. Составим два уравнения:

Решим систему уравнений:

Þ

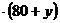11 = 13у

880+11у = 13у

11у – 13у= -880

- 2у = -880

у = -880: (-2)

у = 440

440 – орехов в третьем ящике

х = 80+440

х = 520

520 орехов в первом ящике.

572 ореха во втором ящике.

Ответ: 520, 572, 440 орехов.

Задача 3: После ведения санитарной обработки на базе отдыха количество мух уменьшилось на 9%, а количество комаров – на 4%. В целом количество насекомых уменьшилось на 5%. Сколько процентов от общего числа насекомых составляли комары?

Решение:

Пусть х – было мух, у- было комаров.

0,91х – стало мух после обработки.

0,96у – стало комаров после обработки

0,95(х+у) – стало насекомых после обработки.

Уравнение:

0,91х+0,96у=0,95(х+у)

0,91х+0,96у=0,95х+0,95у

0,96у-0,95у=0,95х-0,91х

0,01у=0,04х

у=4х – следовательно, общее число насекомых 5х, а комаров было 80 % от общего числа насекомых.

Не нашли, что искали? Воспользуйтесь поиском: