Дифференциальные уравнения первого порядка, разрешенные относительно производной. Общие сведения

СРОК СДАЧИ-среда (каф. матем. анализа) 28.10.2015

ВАРИАНТЫ

15. Алейников Р.

16. Герасимов Д.

17. Дубина М.

18. Захарова Е.

19. Козин П.

20. Кульгина В.

21. Немыкина Ю.

22. Пейсахова А.

23. Плещенкова Е.

24. Туркова К.

Замечание: теория и примеры – в помощь. Решаем то, где написано: ЗАДАНИЯ ПО ВАРИАНТАМ:

ЗАДАЧИ № 1-7

Задачи № 1-№ 5. Уравнения первого порядка: с разделяющимися переменными и приводящиеся к ним, однородные и приводящиеся к однородным, линейным уравнения, уравнение Бернулли, уравнение в полных дифференциалах.

Задача № 6. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и указать в общем виде метод решения.

Задача № 7. Смешанные задачи на д.у. первого порядка. Определить тип уравнения и решить.

Дифференциальные уравнения первого порядка, разрешенные относительно производной. Общие сведения

Д.У. первого порядка это равенство, содержащее неизвестную функцию 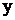, производную 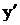и переменную 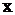, от которой зависит 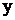. Общий вид д.у. первого порядка

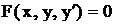(1)

Обычно уравнение (1) стараются представить в форме, разрешенной относительно производной:

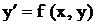(2)

или в форме, содержащей дифференциалы:

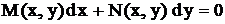(3)

От формы (2) можно перейти к форме (3) и наоборот.

В самом деле, если в уравнении (2) заменить 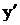через 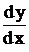, умножить обе части уравнения на 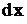и перенести все члены в одну сторону, то получим

,

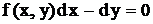Что представляет собой форму (3), где 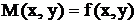, а .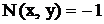

Наоборот, член уравнения (3) вправо и разделить обе части уравнения на 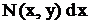, предполагая, что 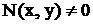, то получим , т.е. форму (2), где .

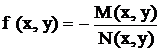Таким образом, Формы (2) и (3) совершенно равноправны, в дальнейшем используется та или другая форма.

Еще раз подчеркнем, что для того, чтобы от формы (2), перейти к форме (3) надо 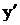записать как отношение 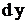и 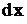, т.е. 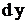деленное на .

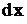Чтобы от формы (3) перейти к форме (2), из равенства (3) надо выразить отношение (частное) .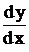

Дифференциальному уравнению удовлетворяет, вообще говоря, целая система функций.

Для выделения одной из них следует указать ее значение при каком-либо значении аргумента 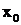, т.е. задать условие вида 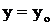при 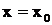, которое называют начальным условием. Часто его записывают в виде

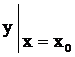
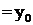(4)

Решение уравнения (2) с условием (4) называют еще задачей Коши.

Решение.

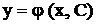(или интеграл 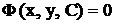) д.у. (2), зависящие от произвольного постоянного С, называется общим решением (общим интегралом) д.у. (2), если путем подбора значений произвольного постоянного из него можно получить частное решение (частный интеграл), удовлетворяющее любому возможному начальному условию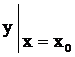 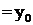. (смотри теоремы существования и единственного решения задачи Коши).

Практически для определения С следует подставить в общее решение (общий интеграл) вместо 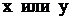заданные значения 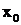и 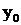и разрешить уравнение

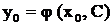
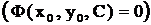
Относительно произвольного С. Пусть 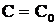, тогда частное решение будет 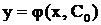(соответственно частный интеграл ).

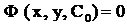Перейдем к рассмотрению отдельных типов дифференциальных уравнений, нахождение общих решений (общих интегралов) которых сводится к выполнению обычных операций вычисления интегралов.

В задачах № 1 - № 5 найти общее решение 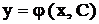или общий интеграл 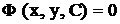и, где указано, решить задачу Коши.

Не нашли, что искали? Воспользуйтесь поиском: