Задача 2. Однородные дифференциальные уравнения.

Дифференциальное уравнение (д.у.)

Называется однородным д.у. относительно 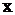и 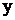, если функция является однородной функцией своих аргументов нулевого измерения. Это значит

. Например функция - однородная

функция нулевого измерения.

Однородное д.у. всегда можно представить в виде

(1)

Введя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющимися переменными:

или переменные разделяются.

Пример 3.

Решить уравнение .

Решение. Запишем уравнение в виде , разделив на 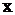обе части уравнения. Сделаем замену . Тогда , 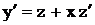. Получим или .

Разделяя переменные, будем иметь .

Отсюда интегрированием находим

или

, так как , то обозначая , получим

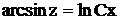. Заменяя на , будем иметь общий интеграл

, отсюда - общее решение.

Ответ: .

Упражнения. Решить уравнения

1. . Ответ: .

2. . Ответ: .

3. . Ответ: .

4. . Соберем коэффициенты при . Ответ: .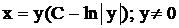

ЗАДАНИЯ ПО ВАРИАНТАМ:

Решить однородные дифференциальные уравнения:

1.	.
2.	.
3.	.
4.	.
5.	.
6.	.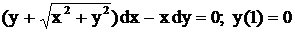
7.	.
8.	.
9.	.
10.	.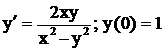
11.	.
12.	.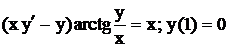
13.	.
14.	.
15.	.
16.	.
17.	.
18.	.
19.	.
20.	.
21.	.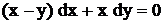
22.	.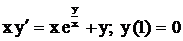
23.	.
24.	.
25.	.
26.	.
27.	.
28.	.
29.	.
30.	.

Не нашли, что искали? Воспользуйтесь поиском: