Уравнение Шредингера в матричной форме.

Уравнение Шредингера:

переходит в следующее:

,

-матричные элементы оператора энергий.

Здесь существует нюанс: оператор в энергетическом представлении должен быть стационарным, т.е. , и тогда удается решить задачу

, (*)

иначе эта задача имеет сложное решение, т.к. там уже .

Решая (*), имеем

.

Очень часто рассматривается представление, в котором энергия диагональна и рассматривается переход от Шредингеровского к Гайзенберговскому описанию. Т.е. у операторов есть временная зависимость и еще мы рассматриваем энергетическое представление, т.е.

.

- переносит временную зависимость на оператор.

- переводит к энергетическому представлению.

Здесь действует фактически один оператор:

.

Тогда оператор

.

,

т.к. операторы и действуют на различные переменные, то они коммутативны, т.е.

,

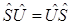тогда

,

.

Но мы знаем, что оператор 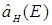сводится к матрице

{оператор (для стационарных : )}= { ; 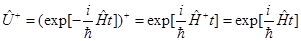, т.к. - унитарный оператор, тогда }=

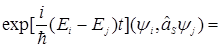= {вводится частота }= .

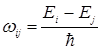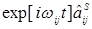Тогда в энергетическом представлении:

Мы получили заготовку для решения задачи о линейном гармоническом осцилляторе.

Для представления Гайзенберга справедливо соотношение:

Уравнение движения

.

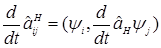Это некое уравнение движения.

Рассмотрим

.

Не нашли, что искали? Воспользуйтесь поиском: