Расчёт основных термодинамических величин фотонного газа.

Мы фактически рассмотрели излучение абсолютно чёрного тела. Электромагнитное поле описывается линейными уравнениями – уравнениями Максвелла, т.е. поля не взаимодействуют друг с другом. Поэтому фотоны между собой не взаимодействуют. А значит, газ фотонов или излучение абсолютно черного тела является идеальным бозе-газом. Но так как масса фотона равна нулю, то имеем ультрарелятивистский случай, а именно:

Но ведь 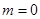, поэтому:

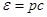- ультрарелятивистский случай

Для фотона пишут энергию:

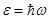
Так как газ ультрарелятивистский, то его уравнение состояния имеет вид:

Конечно, фотоны взаимодействуют и со средой, в которой они находятся. Здесь главное чтобы частоты наполнителя (среды) не совпадали с частотами фотонов, иначе идёт поглащение энергии излучения. В случае несовпадения частот, всё равно идет поглащение, но не столь сильное.

Рассмотрим полость (чёрное тело) в которой вакуум. Но стенки полости взаимодействуют с фотонами, т.е. идёт поглощение фотонов. Так как фотоны исчезают, то их число не сохраняется.

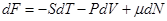
Так как число частиц не сохраняется, то:

даёт - условие равновесия для фотонного газа.

Итак, для фотонов имеем 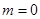и .

Переходим в квазиклассику:

Посчитаем среднее число частиц для такого фотонного газа:

В этом выражении объём 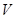появился при интегрировании по координате.

Спин фотона равен нулю, но в данном случае:

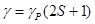
- это член поправки. Это поправка на поляризацию, для электромагнитных волн – две поляризации, тогда , а значит:

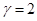- как для электронов, но по другой причине.

Сделаем обозначение:

, тогда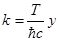

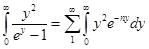
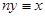
Этот интеграл можно свести к функции Риман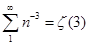а.

, а

Тогда:

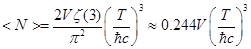
И мы получили среднее число частиц фотонного газа.

Найдём энергию фотонного газа:

Аналогично 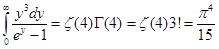, а 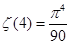. Тогда получаем:

И мы получили среднюю энергию фотонного газа. В термодинамике пишут:

Тогда:

Где - константа Стефана-Больцмана:

- в энергетической шкале

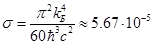- в градусной

- в гауссовой системе единиц.

Можно записать выражения для теплоёмкости фотонного газа:

Другие характеристики:

- для ультрарелятивистского случая

В силу того что :

, ,

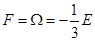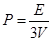
Не нашли, что искали? Воспользуйтесь поиском: