Статистическое описание флуктуаций интенсивного термодинамического параметра.

Рассмотрим вспомогательный вопрос из теории вероятностей. Пусть , где - случайный параметр. Тогда функция - нерегулярная, и если известен закон распределения случайной величины , то можем построить закон распределения для .

Если с некоторой вероятностью лежит в интервале , то лежит в соответствующем интервале с той же вероятностью.

Найдём 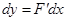. Тогда на языке вероятностей можем записать:

Вообще и 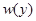- различные функци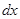и. и берут по модулю, т.к. они могут оказаться отрицательными.

Итак, можем найти:

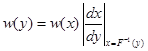
т.е. надо вместо ставить некоторую конкретную функцию , т.к. слева стоит функция от - .

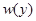Для энергии мы писали:

, где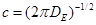

- это случайный экстенсивный параметр, а .

Посмотрим случай, когда флуктуации параметра малы:

В случае малых флуктуации можем функцию 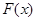разложить в ряд:

, где

У функции в аргументе стоит 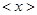и дифференцирование идёт по 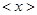, т.е. разложение идёт вблизи этой точки. Если флуктуации малы, то ряд можно оборвать, оставив два слагаемых:

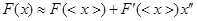
и можем ввести флуктуацию для :

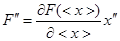
этого выражения бывает достаточно для многих случаев, т.е. когда пренебрегаем остальными членами ряда разложения .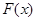

Обозначим , а . Тогда имеем:

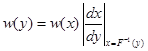
И если 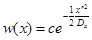, то:

, где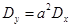

Т.е. получили переход в Гауссово распределение для соответствующих величин.

Теперь рассмотрим переменные энергию и температуру. На ряду с величиной введём величину . и - это термодинамически сопряжённые величины. Такая взаимнообратность справедлива для нашего приближения.

У Ландау записано:

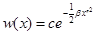, где

Параметр 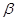- положительный, т.к. энтропия достигает максимума в равновесном состоянии, когда параметры равны средним. В максимуме вторая производная отрицательна.

Запишем для флуктуаций:

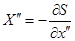
Когда , то и . Найдём флуктуацию :

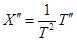
Разложение энтропии в ряд:

Если имеется связь между двумя величинами через некоторый параметр:

или 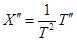, то можем найти флуктуацию и дисперсию температуры.

Мы получили , тогда:

Так как дисперсия известна, то можем получить распределение этой (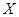) величины. Здесь снова Гауссовский закон.

Отсюда можно получить и и .

Из разложения в ряд вблизи точки и из 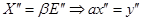пишем распределение для случайной величины :

, где

здесь под понимаем термодинамически сопряжённую величину данной, т.е.

Мы имели , но по нашим переобозначениям имеем . Т.е. мы переобозначили таким образом:

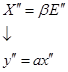
Проверим соотношение из функции :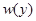

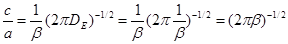
Эта константа имеет размерность температуры, а параметр 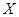имеет размерность обратной температуры.

Таким образом мы посчитали флуктуацию интенсивного параметра 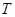. Мы её посчитали через то, что 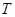есть функция от энергии и наоборот, энергия есть функция температуры. Флуктуация энергии взывает флуктуацию температуры:

Не нашли, что искали? Воспользуйтесь поиском: