Расчет параметров вырожденного электронного газа.

Рассматриваем достаточно низкие температуры, которые удовлетворяют ограничению:

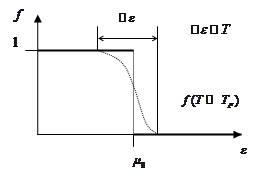
И кривая 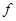незначительно отличается от 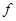при .

Можно качественно оценить величину теплоёмкости для низких температур.

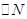- число частиц, охваченных возбуждением.

Тогда:

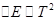
Теплоёмкость :

- при низких температурах

Это качественная оценка теплоёмкости для низких температур.

Т.к. 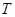мала, то 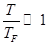- это малый параметр, по которому можно разложить решение.

где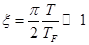

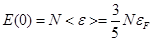
аналогично для химического потенциала:

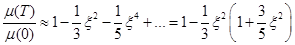
Зная эти поправки можно точно рассчитать теплоемкость:

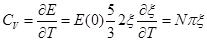
Т.е. с учётом имеем:

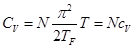
где - теплоемкость на одну частицу.

, ,

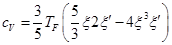
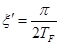Тогда:

- это расчёт с большой точностью

Теперь посчитаем свободную энергию, используя соотношение, связывающее энергию и свободную энергию. В термодинамике имеемся соотношение:

Тогда:

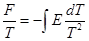
здесь константу вычислять не будем, а будем писать в виде:

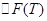- за счёт теплового возбуждения

Тогда:

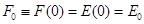
С помощью свободной энергии можем посчитать химический потенциал, энтропию, давление, можно получить уравнение состояния:

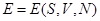
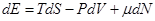
Мы знаем связь и :

, а 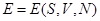, т.е. надо перейти от одних переменных к другим – преобразование Лежандра.

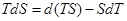
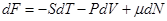
Тогда мы можем найти и как частные производные от по соответствующим переменным:

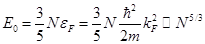
Тогда:

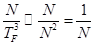
Оказывается, что , тогда:

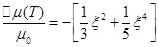
Теперь найдём соотношение для давления:

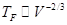
Тогда:

и мы подтвердили зависимость .

Найдём теперь , 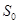- известная величина.

Используем соотношения:

, , ,

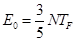Тогда получим:

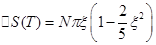
Мы получили температурно-зависящий член энтропии. С ростом температуры энтропия возрастает.

Не нашли, что искали? Воспользуйтесь поиском: