Тензорная функция Грина волнового уравнения.

Рассмотрим

Оператор

Определим тензор Грина оператора равенствами:

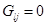, при (*)

, при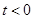

В начале координат в момент времени действует единичная сосредоточенная импульсная сила, плотность которой равна:

(**), - единичный вектор нормали.

Тензор Грина определяет компоненту смещения 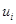, возникающую в точке в момент времени под действием единичного импульса, приложенного в направлении координатной оси в момент времени :

Учитывая (**) получаем:

Вычислим динамический тензор Грина для неограниченной изотропной среды. Воспользуемся интегральными преобразованиями Фурье.

Для изотропной среды оператор :

после преобразования Фурье он примет вид:

А уравнение (*) перейдет в алгебраическое:

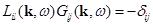
Тогда имеем:

Умножим это выражение на , тогда:

Тогда находим, что:

(***)

Учтем, что и . Тогда перепишем (***) в следующем виде:

Теперь будем осуществлять переход .

Для вычисления интегралов и воспользуемся теоремой о вычетах.

Пусть - угол между и . Обозначим . Введём сферические переменные .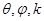

, тогда .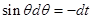

Следовательно .

У этих интегралов есть два полюса: и . Надо использовать при расчёте полюс , чтобы получить физически обоснованную асимптотику. Переходим в комплексную плоскость, замыкаем контур обхода сверху. Используем фиктивный переход:

Это позволяет получить нужную асимптотику.

Применяя теорию вычетов, находим значение интеграла .

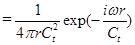
В силу физических соображений знак в экспоненте меняем на “-”.

По аналогии вычислим интеграл .

В силу физических соображений знак в экспоненте меняем на “-”.

Тогда получаем:

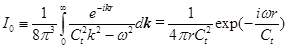
Проводя дифференцирование и используя соотношения:

и , где

Получаем:

,

где

Осуществим переход в пространство оригиналов по времени . Воспользуемся соотношениями:

,

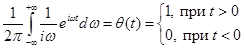
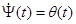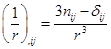
Тогда получаем в итоге:

,

где , при и , при остальных .

Не нашли, что искали? Воспользуйтесь поиском: