Мы писали волновое уравнение в виде

,

здесь

Для одной материальной точки :

1. Без магнитного поля .

2. Если есть магнитное поле, то ,

В этих случаях спин не учтен.

С учетом спина модификацию уравнений сделал Паули.

Примечание: уравнения Шредингера и Паули нерелятивистские.

Запишем уравнение Паули:

.

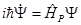
Здесь изменился оператор кинетической энергии.

Без учета магнитного поля

,

где

Здесь

- матрицы Паули

Тогда

.

Покажем, что при отсутствии поля, имеем

,

т. е.

Рассмотрим

={так как действует на спиновую переменную, а на пространственную, то и коммутативны.} = =

={рассмотрим сумму, когда и когда }= ={рассмотрим .

, т. к.

}=[

При :

Рассмотрим случай, когда есть магнитное поле:

.

Тогда для оператора имеем

Тогда оператор кинетической энергии из оператора Паули:

Рассмотрим случай электрона e<0.

(магнетон Бора)

Тогда в итоге получаем:

,

где оператор

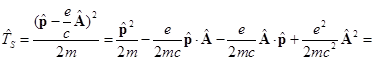
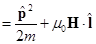
В данном уравнении последний член был опущен ввиду своей малости.

Для оператора Паули тогда получим

,

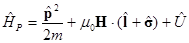Отсюда видно равенство для гиромагнитных соотношений

Видно, что магнитные моменты

,

,

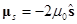механические моменты

Гиромагнитные соотношения

.

Полный магнитный момент

Не нашли, что искали? Воспользуйтесь поиском: