Тензор модулей упругости изотропной среды.

Простейший тензор 4-го ранга – единичный тензор можно разложить на объемную и девиаторную составляющие:

,

где - объемная составляющая, а - девиаторная составляющая.

Видно, что тензоры обладают свойством, аналогичным условию ортонормированности векторных величин:

Для тензоров имеют место соотношения:

,

,

,

т.е. свертка произвольного тензора второго ранга с единичным тензором четвертого ранга оставляет его неизменным. При помощи тензоров и можно разложить тензор второго ранга на объемную и девиаторную составляющие.

Используем представление единичного тензора в виде объемной и девиаторной составляющих для представления тензоров модулей упругости и податливостей изотропной среды в виде:

,

,

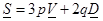где - объемный, а - сдвиговой модули упругости.

Иногда удобна такая запись:

,

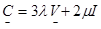
где - постоянная Ламэ.

Податливости выражаются через модули объемной и сдвиговой упругости:

и

По известным модулям упругости могут быть вычислены другие постоянные упругости, например:

модуль Юнга ,

коэффициент Пуассона

Связь между постоянными упругости и модулями и изотропной среды имеет вид:

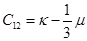
Формулы, выражающие объемный и сдвиговой модули упругости через тензорные свертки величин и :

,

,

Эти соотношения могут быть использованы для вычисления средних модулей упругости поликристаллов.

ГЛАВА 3.

Не нашли, что искали? Воспользуйтесь поиском: