Функционалы, зависящие от производных более высокого порядка

Исследуем на экстремум функционал

где функцию F будем считать дифференцируемой n+2 раза по всем аргументам и будем предполагать, что граничные условия имеют вид

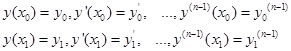
т. е. в граничных точках заданы значения не только функции, но и ее, производных до порядка n-1 включительно. Предположим, что экстремум достигается на кривой у = у(х), дифференцируемой 2n раз, и пусть 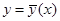— уравнение некоторой кривой сравнения, также дифференцируемой 2n раз.

Рассмотрим однопараметрическое семейство функций

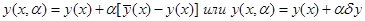
При α = 0 у(х, a) = y(x), при α =1 у(х, a) = 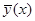Если рассматривать значение функционала 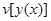только на кривых семейства , то функционал превратится в функцию параметра 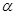, достигающую экстремума при 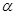а = 0; следовательно,

. Эта производная в соответствии с § 1 называется вариацией функционала v и обозначается ;

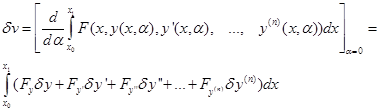
Интегрируем по частям второе слагаемое в правой части один раз:

третье слагаемое — два раза:

и т. д., последнее слагаемое - n раз:

Принимая во внимание граничные условия, в силу которых при

х = х₀ и при х = х₁ вариации δу = δу' = δу" =... =δy^(n-1)=0,

окончательно получим

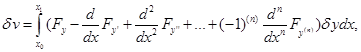
Так как на кривой, реализующей экстремум, имеем

при произвольном выборе функции δу и так как первый множитель под знаком интеграла является непрерывной функцией х на той же кривой у = у (х), то в силу основной леммы первый множитель тождественно равен нулю:

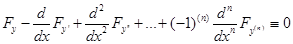
Итак, функция у = у(х), реализующая экстремум функционала

должна быть решением уравнения

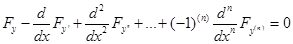
Это дифференциальное уравнение порядка 2n носит название уравнения Эйлера—Пуассона, а его интегральные кривые называются экстремалями рассматриваемой вариационной задачи. Общее решение этого уравнения содержит 2n произвольных постоянных, которые могут быть, вообще говоря, определены из 2n граничных условий:

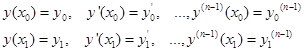
Пример 1. Найти экстремаль функционала

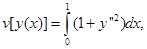
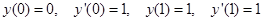
Уравнение Эйлера — Пуассона имеет вид или y^IV = 0;ero

общим решением является . Используя граничные условия, получаем:

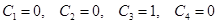
Итак, экстремум может достигаться лишь на прямой у = х.

Пример 2. Определить экстремаль функционала

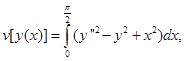
удовлетворяющую условиям

Уравнение Эйлера - Пуассона имеет вид 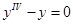его общим решением является 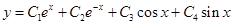. Используя граничные условия, получаем 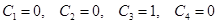. Итак, экстремум может достигаться лишь на кривой у = cos x.

Пример 3. Определить экстремаль функционала

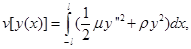удовлетворяющую граничным условиям:

К этой вариационной задаче сводится нахождение оси изогнутой упругой цилиндрической балки, заделанной на концах. Если балка однородна, то ρ и μ постоянны и уравнение Эйлера — Пуассона имеет вид

откуда

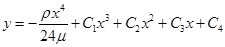
Используя граничные условия, окончательно находим

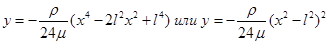
Если функционал v имеет вид

то, варьируя только у(х) и считая z (x) фиксированным, мы находим, что функции у(х) и z(x), реализующие экстремум, должны удовлетворять уравнению Эйлера — Пуассона,

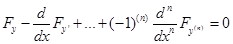
а варьируя z(x) и считая у(х) фиксированным, получим, что те же функции должны удовлетворять уравнению

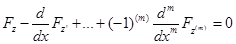
Итак, функции z (x) и у (х) должны удовлетворять системе двух уравнений

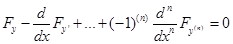
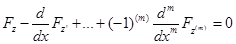
Точно так же можно рассуждать и при исследовании на экстремум функционала, зависящего от любого числа функций:

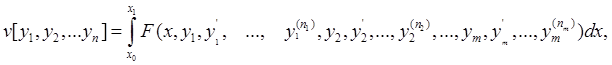
Варьируя какую-нибудь одну функцию y_i (x) и сохраняя остальные неизменными, получим основное необходимое условие экстремума в виде

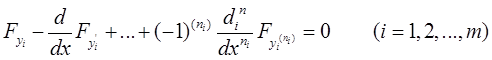
Не нашли, что искали? Воспользуйтесь поиском: