Матричная форма задачи о линейном гармоническом осцилляторе (ЛГО). Матричные элементы операторов в методе Шредингера и Гайзенберга (энергетическое представление).

Запишем оператор для линейного гармонического осциллятора:

,

где оператор 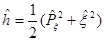– в безразмерных переменных.

Где (1)

(2)

И коммутаторы: (3)

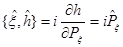(4)

Производная по времени: (5)

(6)

Из (5) и (6) получаем: - это такое уравнение движения.

Можно записать – это уравнение, записанное в методе Гайзенберга, приводит к дисперсному уравнению:

Введём безразмерное время: (*)

Тогда переходит в (10)

где - безразмерная частота.

Тогда (5) ® (7)

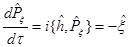(6) ® (8)

И само уравнение движения переходит в:

(9)

и в методе Гайзенберга:

Используя (*) и это уравнение, получаем дисперсионное уравнение:

, которое имеет решение: 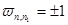и мы записали . Можно записать ещё, что для случая 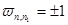. Можно записать таким образом:

(12)

Для (13)

Здесь и здесь присутствует

максимальное из n и n₁

Для матричного элемента 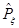получим уравнение: , которое в методе Гайзенберга переходит в

Аналогично (13) можем записать:

Это было получено в V семестре, и надо уметь это получать.

Связь представлений дается в (10), и надо еще учесть, что , тогда в представлении Гайзенберга получим следующие величины: и

Чаще используют и , чем и .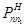

Матричный элемент: (это и для H и для S описания, в энергетическом

представлении).

Напомним, как действует оператор 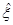в x - представлении и в энергетическом представлении:

Сначала, для произвольного оператора :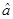

(14) - это в x - представлении

(15) - это в энергетическом представлении или n-представлении,

где n-номер уровня.

В (14) матричный элемент 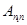выступает в роли разложения функции по базису собственных функций.

В (15) – это матричный элемент в операторном представлении.

Теперь для :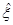

(14)

И аналогично можно записать для оператора :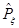

(15), где

Уравнение Паули

Не нашли, что искали? Воспользуйтесь поиском: