Интегральные операторы в квантовой механике.

Оператор в 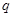- представлении .

В общем случае

Здесь - ядро интегрального оператора в координатном представлении.

Задача на собственные функции и собственные значения

Здесь 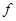и 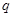изменяются непрерывно.

Разложение функции по базису :

,

где

Тогда

и аналогично

Для того чтобы найти ядро интегрального оператора, разложим - функцию по базису собственных функций из задачи на собственные функции и собственные значения.

={т. к. оператор от q, а интеграл по f, то ставим оператор под знак интеграла} {из задачи на собственные функции и собственные значения }= .

Поменяем порядок интегрирования

Ядро интегрального оператора

Оператору поставили в соответствие ядро . Тогда можно записать действие оператора на любую функцию, решив задачу на собственные функции и собственные значения.

Пусть есть эрмитов оператор

.

Тогда

А в силу равенства имеем

Найдем ядро оператора в координатном представлении. Действие в этом представлении сводится к умножению на .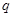

Мы знаем, что по определению -функции:

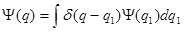
Тогда

Ядро оператора координат в координатном представлении

Ядро оператора в 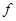-представлении, тогда имеет вид

Не нашли, что искали? Воспользуйтесь поиском: