Интегральный оператор канонического преобразования.

Можно решать задачу в разных представлениях. Преобразование, осуществляющее замену переменных, в которых рассматривается задача, называется каноническим преобразованием.

Запишем:

(*)

(**)

Сравним эти равенства с:

Тогда можно рассматривать как ядро некоторого интегрального преобразования, переводящего 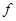- представление в 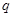-представление.

Обозначим

,

где

Собственная функция оператора в 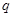-представлении играет роль ядра интегрального оператора 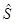, осуществляющего преобразование от к .

Аналогично

Из соотношения (*) следует, что для того чтобы говорить о функции надо знать коэффициенты разложения . Т. е. зная можем записать :

Чтобы знать коэффициенты надо знать - это следует из (**)

Тогда задать состояние мы можем либо функцией , либо функцией . Эту информацию мы задаем в разложении переменных.

Оператор 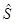осуществляет переход от 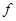переменных к 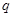переменным:

.

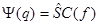Это есть каноническое преобразование переменных.

Установим связь между и :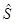

,

,

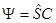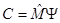подставим одно в другое

,

тогда

(***)

Д.З. записать это равенство на языке ядер.

Распишем:

также

Этому соответствует соотношение операторов

Из (***) следует , тогда

,

отсюда

получили, что оператор 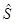унитарный.

Рассмотрим норму функции и обнаружим унитарность:

{используем равенство Парсеваля} ,

тогда , .

Равенство Парсеваля:

.

Мы знаем, что ядро оператора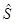

,

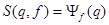есть собственная функция оператора в 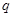- представлении.

Тогда ядро оператора :

,

есть собственная функция оператора в 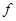-представлении.

Но

.

Задачи на собственные функции и собственные значения имеют вид:

,

.

-собственная функция оператора в 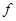-представлении есть комплексно сопряженная собственная функция оператора в 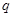- представлении.

Отсюда запишем:

Не нашли, что искали? Воспользуйтесь поиском: