Каноническое преобразование оператора.

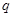Рассмотрим произвольный оператор в - представлении

. (+)

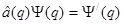В 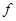-представлении

(++)

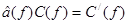Воспользуемся

,

,

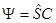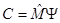тогда

.

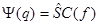Но и

.

Из (+) получим

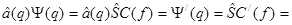{из (++)} .

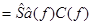Получили равенство

, (+++)

связь между операторами в разных представлениях.

Из (+++) получим модификации (исп. Унитарность ):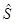

,

.

Или в интегральной форме

(*)

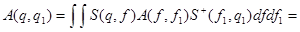={подставим соотношения , }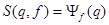

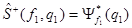Далее

и .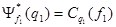

Также

, (**)

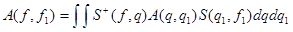здесь .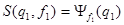

.

И

,

.

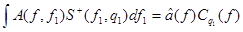
Рассмотрим

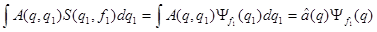
Теперь распишем

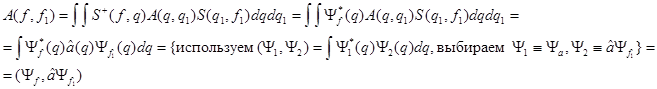
Тогда получили

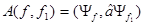(1)

Аналогично

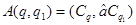(2)

Итак каноническое преобразование имеет вид:

,

где ядро канонического оператора 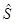имеет вид:

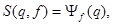
обратное преобразование

,

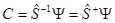где ядро оператора 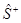имеет вид:

.

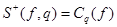Но было также установлено, что

,

тогда установили соответствие

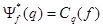
Скалярные произведения из (1) и (2) есть матричные элементы оператора 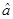для непрерывного спектра.

Унитарные инварианты в квантовой механике.

Оператор унитарный, если

.

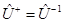Как пример унитарных операторов приведем:

1) 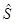- оператор канонического преобразования.

2) 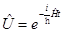- оператор эволюции.

Унитарный инвариант – инвариантность относительно унитарного преобразования.

Докажем, что эрмитовость является унитарным инвариантом.

Пусть

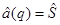и .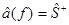

Между представлениями существует связь

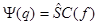
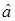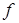Эрмитовость оператора в и 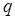представлении означает:

(1)

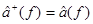(2)

Теперь надо показать, что из (1) следует (2) и наоборот, что из (2) следует (1).

Пусть известно, что 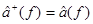, докажем (1).

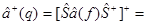{используем, что }

={Используем, что = (*)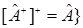

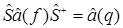Тогда из (2) следует (1). Наоборот, аналогично из (1) следует (2).

Рассмотрим задачу на собственные функции и собственные значения для оператора 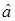и покажем, что спектр этой задачи есть унитарный инвариант.

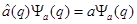(3)

Теперь докажем, что собственное значение удовлетворяет также задаче

Мы знаем, что переход осуществляется по связи

,

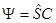тогда имеем

.

Из (3) получаем

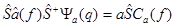
Так как

.

.

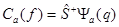Переносим все в левую часть равенства:

.

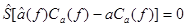Оператор 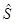не нулевой.

Это задача на собственные функции и собственные значения в 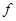представлении с тем же оператором и с тем же собственным значением.

Но справедлив и обратный переход из 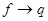представление.

Вывод. Спектр собственных значений оператора – унитарный инвариант.

Спектр собственных значений дает результат измерения физической величины.

Докажем, что норма функции есть унитарный инвариант.

Рассмотрим нормировку на примере канонического преобразования.

Напомним равенство Парсеваля

Равенство Парсеваля означает сохранение нормировки относительно унитарного преобразования.

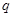Но, по определению, и есть норма функции в и в 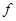- представлении.

Покажем, что среднее значение физической величины есть унитарный инвариант.

По определению среднего:

.

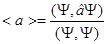Для знаменателя инвариантность доказана.

Распишем числитель

Таким образом

.

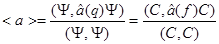Не нашли, что искали? Воспользуйтесь поиском: