Основное состояние атома гелия.

Рассмотрим основное одночастичное состояние:

.

Здесь удобно перейти к атомным (кулононовским) единицам, чтобы исключить константы , , , тогда

.

В кулоновских единицах одночастичная функция для основного состояния выглядит:

.

Каким квантовым числам соответствует одночастичное состояние? Вводят три квантовых числа (без спина): , , 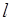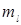. Для основного одночастичного состояния 1, 0, 0 соответственно.

Тогда, ставим индексы

.

Эта функция нормирована на единицу, т. е.

.

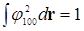Если взять симметричные и антисимметричные функции для двух частиц в основном состоянии, то имеем:

,

.

И получаем, что основное состояние описывает симметричная функция. Вычисление энергии одночастичного состояния для центрального поля мы проводили и получали в размерных единицах

.

Или в кулоновских единицах

.

, .

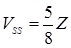Задача

Определить приближенно энергию основного уровня атома гелия (ядро с зарядом Z и два электрона), рассматривая взаимодействие между электронами как возмущение.

Решение

В основном состоянии иона оба электрона находятся в S-состояниях. Невозмущенное значение энергии равно удвоенному основному уровню водородоподобного иона:

.

Поправка первого приближения дается средним значением энергии взаимодействия электронов, взятом по состоянию с волновой функцией

.

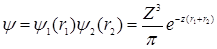(произведение двух водородоподобных функций с )

Интеграл

проще всего вычислить так

,

,

.

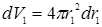Энергия распределение зарядов в поле сферически – симметричного распределения 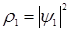. Подынтегральное выражение интеграла по 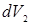есть энергия заряда 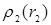в поле сферы 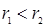. Множитель 2 перед интегралом учитывает вклад от конфигураций, в которых .

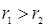Вычислим интеграл .

Для начала определимся с тем, что нам считать за 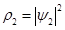и . Из выражения 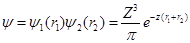следует, что , .

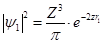Вынося все константы за знак интеграла в итоге получаем:

Обозначим за правую часть интеграла и посчитаем его первым.

Таким образом, получим

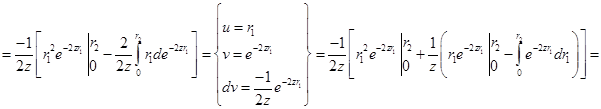
В итоге интеграл I равен:

Подставляя в пределы 0 и 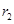получаем:

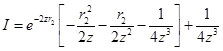
Подставляя интеграл I в наш большой интеграл, получаем:

Вычисляем этот интеграл, разбив его на сумму четырех интегралов:

Для решения данных интегралов нам потребуется определение и свойства гамма-функции:

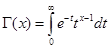- определение гамма-функции

Свойства гамма-функции:

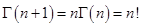
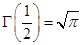
Складывая + + 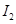+ 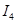, получаем:

.

Когда рассчитываем основное состояние, то функция основного состояния должна быть ,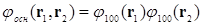

однако, ранее мы получили формулу

.

Мы все это рассчитываем через

(53.1)

Однако, правильный результат получается из

.

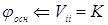Тогда в формуле (53.1) стоит при лишня двойка, которая потом дала .

Так как у нас два электрона, то есть две частицы, то

.

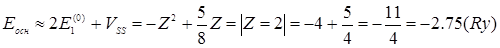В первом приближении, энергия основного состояния для атома Гелия в атомных единицах . В самосогласованном методе решение оказывается: .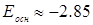

ФАКУЛЬТАТИВ

Не нашли, что искали? Воспользуйтесь поиском: