Уравнение состояния квантового идеального газа. Обменные эффекты.

Уравнение состояния – это уравнение, связывающее переменные .

Мы знаем выражение для свободной энергии Гельмгольца :

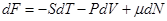
Отсюда удобно получать давление:

Выражение для термодинамического потенциала:

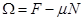
Получив мы сможем найти , тогда сможем получить уравнение состояния. Займёмся расчётом . Мы получали для :

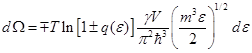
Воспользуемся этим выражением:

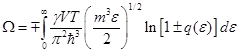
Интегрируем по частям и сводим это выражение к интегрированию по энергии.

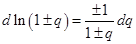, а

Тогда:

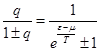
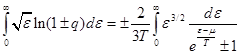
Тогда для получаем:

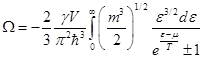
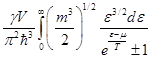- это есть полная энергия системы, тогда:

Теперь имеем соотношения:

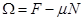
Тогда:

В результате получаем:

Это соотношение выполняется ещё и для классического идеального газа. Но для Больцмановского идеального газа было:

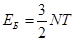, и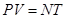

У нас газ – квантовый, поэтому соотношение для боле сложно, оно даётся интегралом:

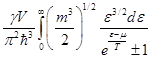
Нам следует рассчитать этот интеграл, он берётся приближенно.

В классическом случае было и 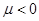. В квантовом случае:

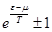- когда в этом выражении пренебрегаем единицей, то получаем Больцмановское распределение. Мы учтём единицу до первого порядка малости. Для этого разложим в ряд:

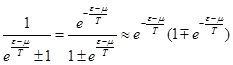
Теперь подставим это в наш интеграл:

Введём переменные:

и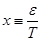

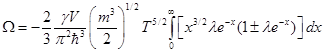
Этот интеграл распадается на два. Первое слагаемое даёт Больцмановскоий результат(классический), а второе дает квантовую поправку, поэтому:

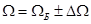
И уравнение состояния:

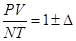
Запишем :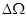

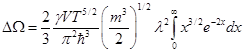
Этот интеграл сводится к гамма-функции. Вводится обозначение:

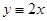, отсюда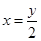

Тогда:

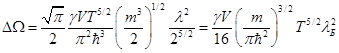
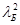- сюда сделаем подстановку Больцмановского приближения химического потенциала .

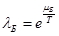Тогда:

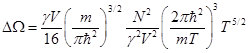
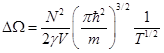
И мы оценили квантовую поправку к термодинамическому потенциалу .

Так как свободная энергия 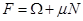, то её можно представить как , т.к. 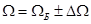, причём, как видно .

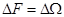Найдём поправку 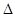к уравнению состояния. Уравнение состояния получается дифференцированием свободной энергии оп объёму :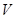

,

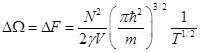
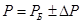
Тогда:

Напомним, что 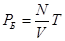- это из уравнения состояния.

Обозначим:

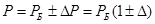
Тогда:

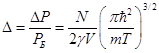
Таким образом, получили уравнение состояния в виде:

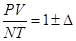
Добавки за счёт квантовых свойств системы оказываются в зависимости от систем частиц различными:

«+» - для Ферми-Дирака

«-» - для Бозе-Эйнштейна.

Это называют обменными эффектами, которые обусловлены симметрией волновых функций(симметрией или антисимметрией – т.е. зависит от спина).

Не нашли, что искали? Воспользуйтесь поиском: