Вырожденный Бозе-газ – квазиклассическое приближение.

Запишем функцию распределения Бозе-Эйнштейна:

, где - номер одночастичного состояния

В квазиклассическом приближении переходим в фазовое пространство:

, - шести мерное фазовое пространство.

Здесь . Полное число частиц в квазиклассическом приближении:

(30)

Так как энергия не зависит от :

то по можно проинтегрировать.

, тогда

Выясняется, что переход (30) не является равенством, поэтому полученный интеграл обозначим как :

Дело в том, что интеграл при нулевых энергиях обращается в нуль, т.к. влечет . Но на самом деле , но - это и зануляет результат при .

Таким образом - это число частиц с положительной энергией .

Полное число частиц:

где - число частиц с нулевой энергией . находится из - надо суммировать по всем состояниям где , а именно:

Это есть некоторая функция от . Для Бозе частиц .

Теперь модифицируем функцию , в ней тоже введём переменную :

Введём переменную , тогда . Тогда:

Можем найти:

Значит и тогда:

Аргумент экспоненты , тогда:

Тогда имеем:

Введём удобную константу:

Константа уже встречалась при расчёте химического потенциала.

Интегрирование по телесному углу даст:

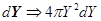
Тогда будем иметь:

где 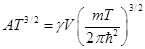, а - функция от

Посмотрим теперь на функцию :

, где

Посмотрим как функции и зависят от . Легко видеть, что:

и

т.е. с ростом эти функции возрастают.

возрастает – это значит что возрастает , т.к. .

Так как 0 отрицательное, то его рост – это значит убывание по абсолютной величине.

Возрастание

Тогда убывание 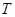приводит к убыванию и следовательно к убыванию функций , и .

Функция имеет некоторый максимум при , т.е. не может превысить нуль. Тогда ограничение для :

так же убывает при убывании .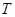

Существует некоторая температура 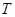при которой равен полному числу частиц . Такая температура называется температурой конденсации . Тогда имеем определение:

, где .

- это функция Римана:

Оказывается, что .

Тогда зная , можем рассчитать температуру конденсации .

Если понизим 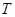ниже , т.е. , то в уравнении

(31)

нет решения для химического потенциала. Это уравнение при заданных и 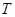является уравнением, определяющим химический потенциал.

Т.е. при не можем вычислить из уравнения (31) классическим образом.

Как решают уравнение (31):

1) при пренебрегают и решают получая

2) при принудительно полагают для оценки

Тогда при имеем:

Тогда разность дает число частиц на нулевом уровне.

Тогда:

И, следовательно, имеем:

- отсюда находим число частиц на нулевом уровне

При все частицы переходят на нулевой уровень энергии.

Речь шла не о реальной конденсации, а о конденсации в импульсном пространстве.

Проводили оценки для парагелия и получали значение температуры:

Это называется - точкой гелия.

Если оценить по нашим формулам, то получится:

Переход всех частиц на основной уровень называют Бозе-Эйнштейновской конденсацией.

Не нашли, что искали? Воспользуйтесь поиском: