Случай нескольких термодинамических параметров.

Вместо одного параметра рассматриваем несколько, тогда и энтропия имеет несколько параметров:

Равновесие наступает при , и в этом состоянии энтропия достигает максимума, тогда флуктуация:

Флуктуация будет фигурировать в разложении энтропии. Энтропию можно разложить в ряд:

Этот ряд Тейлора обрываем на третьем члене, т.е. квадратичном по флуктуациям:

Так как в равновесии энтропия достигает экстремума, то весь набор первых производных обращается в нуль:

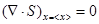
Так как вторая производная является постоянной, то вводим обозначение:

Квадратичная форма, которая построена на тензоре , должна быть положительной:

(*)

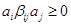Это есть условие максимума энтропии в состоянии равновесия.

Тогда запишем для энтропии, обозначив :

Соотношение (35), если его записать строго, решается проще. Соотношение (*) – есть критерий Сильвестра, оно может быть распространено на все аналогичные образования: и в интегральном исчислении, и в функциональном анализе.

Запишем матрицу:

В силу симметрии .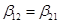

Когда пишем критерий положительной определённости , то должны быть положительны только главные базисные миноры. Когда пишем, то надо перебирать все миноры, что бы они были не отрицательны. В этом состоит условие критерия Сильвестра.

Проще работать со строгим неравенством:

Вероятность реализации параметров:

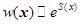
Тогда получаем:

(**)

Критерий применимости этой формулы:

Формула применима с той же точностью, что и приближение .

Таким образом, имеем случай малых флуктуаций.

Формула (**) - это многомерный Гауссов закон.

Не нашли, что искали? Воспользуйтесь поиском: