Аппроксимация Гауссовым законом распределения вероятностей для экстенсивного термодинамического параметра.

Так как энтропия достигает максимума при наиболее вероятном значении соответствующей термодинамической величины, то закон для этой величины может быть получен методом аналогичным как для энергии. Речь идёт об экстенсивных величинах (например об энергии).

Тогда обозначая эту величину через x можем записать вероятность того, что термодинамическая величина x лежит в интервале как:

- это плотность вероятности

в случае энергии мы обозначали как

Константу найдём из условия нормировки:

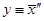
Тогда:

Итак, имеем:

Введём критерий применимости квазиклассического приближения к описанию термодинамических величин. Существует такое соотношение неопределённости:

где - время релаксации, а - неопределённость энергии.

Используем это соотношение для нахождения неопределённости в нахождении энтропии.

Из соотношения получаем неопределённость энтропии :

Тогда имеем:

Поскольку энтропия входит в плотность вероятности:

то неопределённость не должна приводить к влиянию на вероятность термодинамической величины . Поэтому должно выполнятся

Тогда для времени релаксации находим:

т.е. при таком ограничении можем применять квазиклассику в термодинамике.

, ,

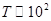
Тогда 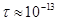при комнатной температуре.

Не нашли, что искали? Воспользуйтесь поиском: