Многомерное Гауссово распределение.

Мы получили:

Теперь следует получить константу. Если записать матрицу 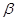в главных осях, то она диагонализируется, формула (36) упрощается.

Запишем новые переменные:

, где - это матрица преобразования координат.

Тогда получаем:

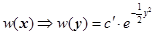(37)

Легко видеть, что

Рассмотрим :

Имеем условие нормировки

Из него и находим константу .

Имеем

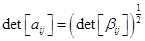
У Ландау записано . Можем записать аналогично:

Ланаду понимает под 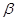определитель .

Рассмотрим термодинамически сопряженные величины, которые вообдятся соотношением:

Можно найти такие средние:

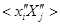- это как смешанные моменты

У Ландау записан результат для частного случая:

Хотя результат можно получить несколько иначе. Запишем среднее:

(*)

Продефференцируем равенство (*):

Мы знаем, что:

Тогда:

В результате имеем:

Тогда имеем:

и можем автоматически дописывать :

Теперь если заменить на , тогда получим:

Если слева и справа умножить это выражение на матрицу, обратную к 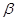, то получим:

т.е. матрица, обратная к 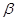есть матрица дисперсий, или матрица ковариаций.

Не нашли, что искали? Воспользуйтесь поиском: