Метод (представление) Гайзенберга. Уравнение движения для оператора.

Существует подход Гайзенберга: рассмотрим волновую функцию как волновую функцию в некоторый момент времени , т.е. -функция фиксированная во времен.

,

тогда

,

где

- функция в представлении Шредингера.

- функция в представлении Гайзенберга.

Но система меняется во времени. Тогда изменение квантовой системы должно быть связано с изменением оператора .

Из унитарности следует

.

Напомним, что в теории представления было следующее. Преобразование функции

порождает следующее преобразование оператора

.

Как мы видим в представлении Гайзенберга функция явно от времени не зависит, но тогда от времени зависит оператор

.

А в подходе Шредингера была явная зависимость волновой функции от времени, а оператор от времени явно не зависел.

Дифференцируем оператор по времени

(**)

теперь запишем уравнение для оператора эволюции

Сопряженное уравнение

Тогда имеем

,

.

Подставляем эти уравнения в (**), получаем

={теперь видно, что в каждом слагаемом есть и , а их можно вынести за скобки}

={внутри квадратных скобок стоит оператор, над которым осуществляется преобразование, причем

,

}=

.

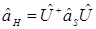Получили уравнение движения для оператора

Представление Шредингера более физично и более распространено.

Представление Гайзенберга рассматривается только в некоторых системах.

При переходе из одного представления к другому результаты физических наблюдений не меняются. Эти представления унитарные инварианты.

Рассмотрим

.

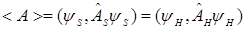Найдем

Производная от среднего есть средняя от производной.

Заметим, что под скобками <> можно писать как S, так и H, т.к. среднее инвариантно относительно преобразования.

E – представление.

E – представление – это представление в котором матрица энергий диагональная. Так как оператор имеет дискретный спектр, то мы рассматриваем дискретный случай.

.

Здесь надо решить ЗШЛ в координатном представлении.

Матричный элемент

.

Матрица оператора :

.

Матрица энергий диагональна.

Мы говорим, что - функция - это функция полного набора динамических переменных и времени.

Если в качестве одной из переменных возьмем энергию, то останется переменная.

Рассмотрим

.

(*)

Часто пишут

,

хотя на самом деле

.

Будем опускать аргумент 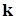, записывая

,

где 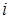- номер значения энергии .

Каноническое преобразование (*) – это смена представлений: перешли от - представления к - представлению. Здесь уже роль волновой функции играют коэффициенты .

Соответственно этому преобразованию волновых функций преобразуются операторы:

.

То же на языке ядер, опустив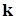

,

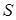- это собственные функции оператора энергии в координатном представлении.

Можно записать:

,

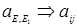т.к. спектр дискретный.

Тогда роль ядра оператора 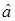в - представлении играет матрица .

Таким образом, мы переходим от к и от к .

Если рассматривать действие оператора “ 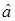” на функцию “ ”, то имеем

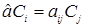
Коэффициенты , т.е. определяются как:

,

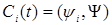где

- собственная функция оператора энергии,

- зависит от времени, т.е. .

Не нашли, что искали? Воспользуйтесь поиском: