Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства.

Напомним некоторые результаты из теории представлений.

Рассмотрим волновую функцию = и разложим эту функцию в интеграл по собственным функциям оператора

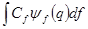= ; - ЗШП для

где - эти функции удовлетворяют условию нормировки:

Перепишем интеграл:

= =

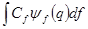т.е. собственную функцию оператора в представлении обозначили:

тогда получаем:

= { некоторое интегральное соотношение, которое

можно записать как действие оператора на

функцию в других переменных } =

Это некоторое каноническое преобразование, которое осуществляется с помощью оператора с ядром .

Имеем преобразование вида

Переменные 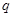и 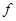указаны в ядре оператора и оператор – унитарный, он не нарушает правила нормировки.

Определение унитарного оператора : .

Существует обратное преобразование:

Функция – это функция в 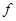– представлении

Как коэффициент разложения в интеграл, она получается:

И дальше будем писать , чтобы подчеркнуть, что – это не столько коэффициент разложения, сколько функция , а 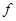– это её аргумент.

Как всё это скажется на произвольном операторе?

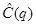- это оператор, действующий в 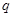представлении

- получили новую функцию в тех же переменных.

Запишем это в форме ядра:

C другой стороны, можем разложить по базисным функциям, которые использовали вначале:

Коэффициенты разложения определяются: , подставим сюда

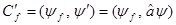, тогда:

т.е. , где

Используя, что и ещё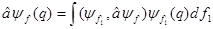

вводится обозначение: тогда

Тогда получим:

здесь всё в здесь функция в координатном пред-

q - представлении ставлении, а ядро оператора и интег-

Не нашли, что искали? Воспользуйтесь поиском: