Это для представления Гайзенберга, причём , т.к. .

Тогда уравнение 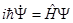- идёт к - описанию.

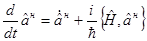- идёт к -описанию.

Представления Шредингера и Гайзенберга равнозначны.

Мы рассмотрим методы Шредингера и Гайзенберга в случае энергетического

представления (в случае дискретного спектра).

Чаще используется метод Шредингера, но мы рассмотрим оба метода.

Мы переходим к энергетическому представлению, это значит, что мы переходим

от функций перемен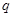ных к функциям переменных (так как спектр

дискретный) .

Напомним полученные формулы:

Для Шредингера: 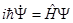- временная зависимость заключена в волновой функции, а оператор 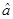таков, что .

Для Гайзенберга – временная зависимость переносится с функции на оператор:

.

Уравнение функции движения для оператора:

,

которое в частном случае переходит в коммутатор при

Мы рассматриваем Энергетическое представление, т.е. одной из динамических

переменных выбрана энергия:

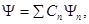где

Вообще переход от к можно рассматривать как каноническое преобразование: .

А произвольный оператор 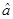в другое представление переходит через преобразование .

Для дискретного случая ядро переходит в - матричный

элемент. По определению матричного элемента

Используем в энергетическом представлении представления и .

Запишем матричный элемент оператора :

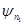={ – собственная функция оператора }=

= - матрица энергий диагональная в собственном представлении.

Тогда уравнение Шредингера в методе Шредингера:

Вместе с здесь

Ещё другие

Динамические

Переменные

Получили уравнение Шредингера в методе , в энергетическом представлении.

Если задача стационарная, то от времени и получаем

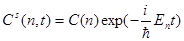
Рассмотрим метод Гайзенберга, здесь используется оператор эволюции :

Это соотношение переходит в случае дискретного энергетического спектра:

, (1)

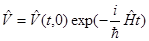где , при .

Если рассмотреть , и матричный элемент тогда имеет вид:

- диагональный вид.

Тогда (1) перепишется:

.

Т.е. - получим связь через оператор эволюции.

Рассмотрим матричные элементы:

(**)

Найдём 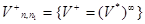={ в силу симметрии оператора }=

(*)

Подставим (*) в (**)

при суммировании

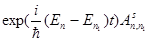– это матричный элемент в представлении Гайзенберга.

Введём , тогда матричный элемент в представлении Гайзенберга

Получим производную от матричного элемента:

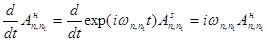
Не нашли, что искали? Воспользуйтесь поиском: