Оператор f в - представлении.

a) Действие оператора на функцию , в - и -представлениях.

Запишем формулы:

,

оператор действуя на переводит ее в функцию . Функцию можно разложить по базису функций : (*)-- суммирование по числам заполнения одночастичных состояний.

Коэффициенты разложения представляют собой матричные элементы: - числа заполнения в одночастичном состоянии.

Это было в - представлении.

Посмотрим действие в -представлении.

Разложим по базису:

эта матрица есть оператор в -представлении.

b) Разложение функции по одночастичным состояниям .

- описывает весь ансамбль частиц

- функция одночастичного состояния.

Напомним, что и .

Для одночастичной функции писали уравнение: ,

функции - образуют базис, по ним можно разложить функцию одной переменной. Но функция N-переменных. Размножим ее по базису в интеграл: - вообще эти коэффициенты есть функция

оставшихся от аргументов, а именно - это есть матричные элементы:

(1) – интегрирование и суммирование по одной переменной (интегрирование по и суммирование по ), при интегрировании и суммировании i-тая координата выходит. Приведем интеграл (1 стр. 23б) к более простому виду, для этого вспомним, что: (2)

Вспомним условие нормировки дл одночастичных функций: ;

i – индекс указывает переменную, по которой идет интегрирование.

В формуле (2) имеется одна функция т.е. из надо выделить функцию , которая соответствует из 1 стр. 23б лекции: ).

Модифицируем :

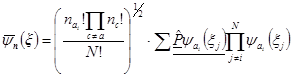
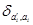В сумму условия нормировки, беря интеграл (1 стр 23 б лекции): ) получим множитель , и еще останется некоторая функция от оставшихся от интегрирования переменных, а именно:

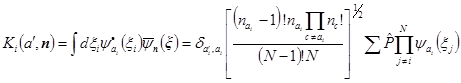
эта часть содержит N-1

частицу, уже просматривается

волновая функция,

описывающая N-1 частицу.

Обозначение: - означает, что здесь не хватает 1-частицы в a-том состоянии, а именно: , тогда как было

тогда имеем, положив , чтобы ,

Запись означает, что в наборе нет переменной , т.к. она стоит после “;”.

Запишем с учетом полученного:

- суммирование по всем одночастичным состояниям, состояния от индекса i не зависят, поэтому a_i писать нехорошо, и i убирают к функции.

c) Матричный элемент одночастичного оператора: 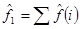, - оператор действующий на переменные i-той частицы: .

Запишем этот матричный элемент в форме скалярного произведения:

т.к. функции симметричны по перестановке частиц, а оператор не зависит от i-той частицы, то получаем умножение на число частиц N и берем любую i из N

сюда надо поставить в виде (2)

произойдет разделение переменных, i-тая переменная выделится, а остальные переменные останутся вместе.

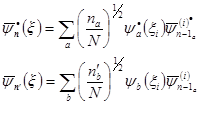
Пусть (3)

(4)

a и b – это наборы одночастичных состояний (5)

и - это наборы чисел заполнения.

Сократить

Оставшееся интегрирование есть скалярное произведение: - здесь у функций убрали индекс (i), т.к. в скалярном произведении стоят симметричные функции, и индекс (i) можно не указывать. Тогда, запишем матричный элемент: .

Мы имели условие ортонормы.

________

, чтобы это скалярное произведение было не ноль, требуется чтобы соответствующие числа заполнения совпадали:

т.е. нужно, чтобы:

Тогда

В этом случае имеем для чисел заполнения:

введем число n_c, когда c≠a,b, для этого числа имеется равенство а для состояний a и b имеются равенства:

тогда имеем матричный элемент

в виде:

d) Матричные элементы

Рассмотрим матричный элемент такого вида:

(6)

Теперь рассмотрим матричный элемент, транспонированный:

(7)

Теперь рассмотрим матричный элемент комплексно сопряженный и транспонированный и с индексом a:

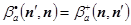
В (7) в силу вещественности этих матричных элементов.

Тогда имеем

Можем упростить выражение для (см стр. 26 б ), для этого вспомним произведение матриц: , т.е.

Тогда имеем , т.е. мы имеем:

Не нашли, что искали? Воспользуйтесь поиском: