Схема Юнга квантовой механики.

Мы рассматривали систему двух электронов. Волновая функция системы двух электронов была:

.

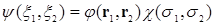Т. е. в гамильтониане не учтен спин и мы можем разделить переменные.

Возможно два варианта:

1. 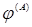и ,

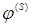2. и .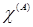

Тогда, мы учитывая принцип тождественности, неявно учитывали спин в теории.

Распространим этот принцип на систему с большим числом электронов.

Так как у электрона два значения спина 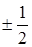, то вводится схема Юнга.

Обозначения:

По горизонтали проводят симметризацию, а по вертикали антисимметризацию.

Будем обозначать цифрами координаты. Пусть есть 3 частицы, тогда:

.

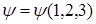Подействуем операторами перестановки:

. (*)

Теперь рассмотрим

, (**)

В результате получаем, что разность (*) и (**) не равна нулю

.

Это значит, что соответствующие величины одновременно не измеримы, у них нет общего базиса и они не могут быть вместе приведены к диагональному виду. То, что у этих операторов различные базисы, т. е. различные собственные функции и показывает, что симметризация не может быть такой простой, как для двух электронов. Задача симметризации относится уже к теории групп.

Вообще говоря, - антисимметричная, т. к. мы рассматриваем фермионы.

Тогда, имеем:

: соответствует

: соответствует :

Здесь координаты не ставят, т. к. рассматривают перестановки по всем координатам, а потом выбирают независимые. Т. е. рассматривают просто схемы симметризации.

Суммарному спину соответствует рисунок

и : ,

а суммарному спину 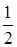соответствует

: соответствует :

При большем числе электронов картина становится следующей:

		Спин

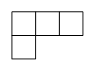
Мы можем установить взаимоодназначное соответствие между картинкой симметрии и спином . Хотя спин в оператор не входит, мы его вводим через принцип тождественности.

Не нашли, что искали? Воспользуйтесь поиском: