Метод (представление) Шредингера. Оператор эволюции и его свойства.

Существует два подхода к описанию квантово-механических систем. Согласно одному из них эволюция описывается с помощью временной зависимости волновой функции. А согласно другому – с помощью временной зависимости оператора, а волновая функция фиксирована.

В классической механике движение системы описывается движением фазовой точки по фазовой траектории. В классической механике существует понятие канонического преобразования переменных: мы можем не говорить конкретно о динамическом импульсе и динамической координате , т. к. существует каноническое преобразование от одних координат к другим

Движение материальной точки можно описывать с помощью канонического преобразования от координат в начальный момент времени к координатам в конечный момент времени. Т. е. эволюция классической системы может быть описана с помощью канонического преобразования.

Мы имеем уравнение Шредингера

.

Оно позволяет найти волновую функцию, описывающую эволюцию системы.

.

Но существует и

,

где - начальный момент времени.

Существует преобразование, которое описывает эволюцию системы:

. (*)

Зная оператор можем перейти из начального состояния в конечное.

Подставим (*) в уравнение Шредингера

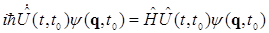
Отметим, что - неявно зависит от динамических координат

Далее переносим все в одну часть и выносим волновую функцию за скобки

Более сложный случай, когда оператор зависит от времени, т. е. внешнее поле нестационарное. Уравнение (33.1) просто решить не удается.

Будем рассматривать случай стационарного поля, когда

Для этого случая оператор имеет вид:

Мы рассматриваем способ описания Шредингера, в котором временная зависимость заключена в -функцию. Эту зависимость можно перенести на оператор эволюции и свести нахождение -функции на нахождение оператора .

В большинстве случаев операторы явно не зависят от времени.

.

Тогда возникает ситуация, когда зависит от времени. Тогда вся информация об эволюции заключена в функции или в операторе эволюции.

Свойства оператора эволюции:

1. Он удовлетворяет уравнению

,

2. при ,

3. - унитарный оператор.

Докажем это

Уравнение обеспечивает сохранение нормы, т.е.

.

Норму можно взять в любой момент времени. Подставим в условие нормировки уравнение (1), причем положим , тогда

.

Таким образом

,

- унитарный оператор.

Не нашли, что искали? Воспользуйтесь поиском: