Тензор дисторсии. Тензор деформаций.

Пусть - радиус-вектор в недеформированном состоянии, а - радиус-вектор после деформации. Вектором смещения будем называть вектор (когда , то это случай параллельного смещения тела как целого). Для описания деформированного состояния следует рассмотреть производную смещения по координате:

- тензор дисторсии

Тензор дисторсии можно представить в виде суммы симметричной и антисимметричной составляющих:

(*) – тензор поворота или вращения

(**) – тензор малых деформаций

Величины - безразмерные.

В соответствии с (*) диагональные элементы тензора вращения равны нулю, а из шести недиагональных независимыми будут только три:

На базе антисимметричного тензора можно построить дуальный ему псевдовектор:

Есл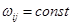и (и ), то имеем поворот тела как целого. Если , то разные точки тела поворачиваются на разный угол, получаем деформацию.

Рассмотрим тензор малых деформаций . При имеем диагональные компоненты тензора, они отвечают за относительное удлинение. При имеем недиагональные компоненты, они отвечают за изменение формы тела.

Сумма диагональных элементов тензора деформаций есть инвариант, и . Величина описывает относительное изменение объема деформированного тела:

Если из тензора деформаций вычесть сумму диагональных элементов по соотношению:

,

то получим тензор девиатор тензора деформаций. Сумма диагональных элементов 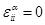. Тензор девиатор тензора деформаций 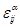описывает изменение формы деформированного тела.

Тензор напряжений.

При деформации тело выводится из положения равновесия. Это приводит к возникновению сил, стремящихся вернуть тело в состояние равновесия. Эти, возникающие при деформации, внутренние силы определяют внутренние напряжения. Силы, определяющие внутренние напряжения, являются близкодействующими.

Выделим в теле некоторый объем и рассмотрим действующую на него суммарную силу, которую можно представить в виде объемного интеграла:

,

где - сила, действующая на единицу объема тела.

Искомую результирующую силу можно рассматривать как сумму только тех сил, которые действуют на данный объем со стороны окружающих его тел, т.е. сил, действующих на каждый элемент поверхности объема (интеграл по некоторой поверхности). Тогда для любого тела каждая из трех компонент равнодействующей всех внутренних напряжений, может быть преобразована в интеграл по поверхности этого объема:

Вектор должен являться дивергенцией некоторого тензора второго ранга, т.е.

Тогда сила, действующая на рассматриваемый объем:

,

где - компонента вектора , направленного по внешней нормали.

Тензор называется тензором напряжений. Выражение есть -тая компонента силы, действующей на элемент поверхности . Сила, с которой рассматриваемый объем действует на окружающую поверхность:

Пример 1.

Запишем тензор напряжения для равномерного всестороннего сжатия тела. Здесь на каждую единицу поверхности действует одинаковое давление , направленное по нормали к поверхности внутрь объема. Тогда на элемент поверхности действует сила 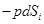, но эта сила должна иметь вид . Написав 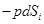в виде , замечаем, что искомый тензор .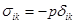

Пример 2.

В равновесии силы внутренних напряжений взаимно компенсируются в каждом элементе объема, т.е. . Тогда уравнение равновесия деформированного тела имеет вид:

Пример 3.

Если тело находится в поле сил тяжести, то уравнение равновесия имеет вид:

,

где 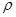- плотность, а - ускорение силы тяжести.

Пример 4.

В случае внешних сил , действующих на единичную площадь поверхности, имеем:

,

но , где - единичная внешняя нормаль. Тогда:

Девиатор тензора напряжений имеет вид:

Девиатор тензора напряжений характеризует сдвиг.

Закон Гука.

Тензоры напряжения и деформаций могут быть определены через термодинамические характеристики – свободную энергию и термодинамический потенциал Гиббса единицы объема среды:

и (*)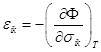

В линейной теории упругости для изотермических процессов величины и могут быть представлены в виде квадратичных форм:

(**),

где - тензор модулей упругости, - тензор податливостей.

Здесь в недеформированном состоянии . Подставляя (**) в (*) получаем:

- обобщенный закон Гука для анизотропных материалов в тензорной форме

Из этих выражение можно получить связь тензоров модулей упругости и податливости . В компонентах:

,

где - единичный тензор.

В общем случаем эти тензоры содержат по 81 компоненте, каждая из которых характеризует упругие свойства тела вдоль определенного направления.

Однако, из-за симметрии физического мира:

,

что позволяет снизить количество независимых компонентов до 21.

Наряду с тензорной формой записи обобщенного закона Гука используется его матричная запись:

,

где 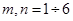. Для матричной формы имеется симметрия:

При использовании матричной формы записи всегда принимается, что оси ортогональной декартовой системы координат согласованы с кристаллографическими осями. Переход от тензорной к матричной форме записи осуществляется объединением двух индексов в один по правилу:

Тензорное обозначение: 11 22 33 23,32 31,13 12,21

Матричное обозначение: 1 2 3 4 5 6

Обычно используют в качестве деформаций сдвига – техническую деформацию, представляющую собой тангенс угла сдвига. Поэтому деформация при в два раза больше, чем соответствующая величина :

, где m=

При переходе к матричному описанию :

При переходе к матричному описанию :

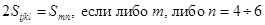
Если учитывать симметрию кристалла, отнесенного к определенному кристаллографическому классу, то число независимых коэффициентов можно ещё уменьшить. Например, для кубической сингонии имеется 3 независимые компоненты тензора четвертого ранга. Матрицы и имеют в этом случае вид:

оотношения между коэффициентами матриц и для кубической сингонии:

Не нашли, что искали? Воспользуйтесь поиском: