
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вариация и ее свойства.
Методы теоретической и математической физики
(конспект лекций для ЭКТ-50М)
Г.
Оглавление
ГЛАВА 1. 4
Введение. 4
§ 1.1 Вариация и ее свойства. 6
§ 1.2 Уравнение Эйлера. 10
§ 1.3 Функционалы вида  .......................................... 14
.......................................... 14
§ 1.4 Функционалы, зависящие от производных более высокого порядка. 16
§ 1.5 Задача о брахистохроне. 19
§ 1.6 Задача Дидоны. 22
ГЛАВА 2. 24
§2.1 Тензор напряжения и деформации. 24
§2.2 Тензор дисторсии. Тензор деформаций. 25
§2.3 Тензор напряжений. 26
§2.4 Закон Гука. 27
§2.5 Тензор модулей упругости изотропной среды. 29
ГЛАВА 3. 31
§3.1 Интегральные операторы в квантовой механике. 31
§3.2 Интегральный оператор канонического преобразования. 32
§3.3 Каноническое преобразование оператора. 34
§3.4 Унитарные инварианты в квантовой механике. 35
§3.5 Матричная форма задачи о линейном гармоническом осцилляторе (ЛГО). Матричные элементы операторов 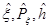 в методе Шредингера и Гайзенберга (энергетическое представление). 37
в методе Шредингера и Гайзенберга (энергетическое представление). 37
§3.6 Уравнение Паули. 39
§3.7 Обменное взаимодействие. 41
§3.8 Основное состояние атома гелия. 44
ФАКУЛЬТАТИВ.. 48
§1 Упругие волны в изотропной среде. 48
§2 Тензорная функция Грина волнового уравнения. 49
§3 Уравнение состояния квантового идеального газа. Обменные эффекты. 52
§4 Расчет параметров вырожденного электронного газа. 55
§5 Вырожденный Бозе-газ – квазиклассическое приближение. 58
§6 Плотность вероятности для энергии системы, описываемой каноническим распределением Гиббса. 61
§7 Аппроксимация Гауссовым законом распределения вероятностей для экстенсивного термодинамического параметра. 64
§8 Статистическое описание флуктуаций интенсивного термодинамического параметра. 65
§9 Случай нескольких термодинамических параметров. 67
§10 Многомерное Гауссово распределение. 69
§11 Расчёт флуктуаций термодинамических величин. 70
§12 Расчет термодинамических величин вырожденного Бозе-газа. 71
§13 Расчёт основных термодинамических величин фотонного газа. 75
§14 Метод (представление) Шредингера. Оператор эволюции и его свойства. 77
§15 Метод (представление) Гайзенберга. Уравнение движения для оператора. 78
§16 E – представление. ………………80
§17 Уравнение Шредингера в матричной форме. 81
§18 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства. 82
§19 Энергетическое представление в случае дискретного спектра: методы Шредингера и Гайзенберга. 85
§20 Операторы рождения и уничтожения в задаче о ЛГО (линейном гармоническом осцилляторе). 87
§21 Свойства оператора рождения и уничтожения. 88
§22 Волновая функция в  - представлении. 90
- представлении. 90
§23 Оператор f в  - представлении. 93
- представлении. 93
§24 Операторы рождения и уничтожения частиц. 96
§25 Схема Юнга квантовой механики. 98
ГЛАВА 1.
Введение.
Наряду с задачами, в которых необходимо определить максимальные и минимальные значения некоторой функции  в задачах физики нередко возникает необходимость найти максимальные или минимальные значения величин особого рода, называемых функционалами.
в задачах физики нередко возникает необходимость найти максимальные или минимальные значения величин особого рода, называемых функционалами.
 Функционалами называются переменные величины, значения которых определяются выбором одной или нескольких функций. Например, функционалом является длина
Функционалами называются переменные величины, значения которых определяются выбором одной или нескольких функций. Например, функционалом является длина  дуги плоской (или пространственной) кривой, соединяющей две заданные точки
дуги плоской (или пространственной) кривой, соединяющей две заданные точки 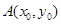 и
и  (см. рис. А). Величина
(см. рис. А). Величина  может быть вычислена, если задано уравнение кривой
может быть вычислена, если задано уравнение кривой  ; тогда
; тогда

Площадь  некоторой поверхности также является функционалом, так как она определяется выбором поверхности, т. е. выбором функции
некоторой поверхности также является функционалом, так как она определяется выбором поверхности, т. е. выбором функции 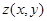 , входящей в уравнение поверхности
, входящей в уравнение поверхности  . Как известно,
. Как известно,

где D — проекция поверхности на плоскость Оху.
Моменты инерции, статические моменты, координаты центра тяжести некоторой однородной кривой или поверхности также являются функционалами, так как их значения определяются выбором кривой или поверхности, т. е. выбором функций, входящих в уравнение этой кривой или поверхности.
 Во всех этих примерах мы имеем характерную для функционалов зависимость: функции (или вектор - функции) соответствует число, в то время как при задании функции
Во всех этих примерах мы имеем характерную для функционалов зависимость: функции (или вектор - функции) соответствует число, в то время как при задании функции  числу соответствовало число.
числу соответствовало число.
Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения функционалов. Задачи, в которых требуется исследовать функционал на максимум или минимум, называются вариационными задачами.
Многие законы механики и физики сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать минимума или максимума. В такой формулировке эти законы носят название вариационных принципов механики или физики.
К числу таких вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии, закон сохранения импульса, закон сохранения количества движения, закон сохранения момента количества движения, различные вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике, принцип Кастилиано в теории упругости и т. д.
Вариационное исчисление начало развиваться с 1696 года и оформилось в самостоятельную математическую дисциплину с собственными методами исследования после фундаментальных работ действительного члена Петербургской Академии наук Л. Эйлера (1707 —1783 г.), которого с полным основанием можно считать создателем вариационного исчисления.
Большое влияние на развитие вариационного исчисления оказали следующие три задачи:
Задача о брахистохроне. В 1696 году Иоганн Бернулли опубликовал письмо, в котором предлагал вниманию математиков задачу о линии быстрейшего ската — брахистохроне. В этой задаче требуется определить линию, соединяющую две заданные точки А к В, не лежащие на одной вертикальной прямой, и обладающую тем свойством, что материальная точка скатится по этой линии из точки А в точку В за кратчайшее время (рис. Б).
Легко видеть, что линией быстрейшего ската не будет прямая, соединяющая точки А и В, хотя она и является кратчайшим расстоянием между точками А и В, так как при движении по прямой скорость движения будет нарастать сравнительно медленно; если же мы возьмем кривую, более круто спускающуюся около точки А вниз, то хотя путь и удлинится, но значительная часть пути будет пройдена с большей скоростью. Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Оказалось, что линией быстрейшего ската является циклоида.
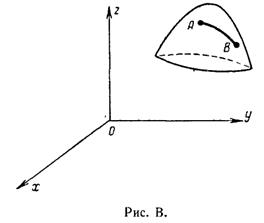 Задача о геодезических линиях. Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности
Задача о геодезических линиях. Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности  (рис. В). Такие кратчайшие линии называются геодезическими.
(рис. В). Такие кратчайшие линии называются геодезическими.
Мы имеем типичную вариационную задачу на так называемый связанный или условный экстремум. Необходимо найти минимум функционала

причем функции  и
и  должны быть подчинены условию
должны быть подчинены условию  . Эта задача была решена в 1698 году Я. Бернулли, но общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.
. Эта задача была решена в 1698 году Я. Бернулли, но общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.
Изопериметрическая задача. Требуется найти замкнутую линию заданной длины  , ограничивающую максимальную площадь
, ограничивающую максимальную площадь  . Такой линией, как было известно еще в древней Греции, является окружность. В этой задаче требуется определить экстремум функционала
. Такой линией, как было известно еще в древней Греции, является окружность. В этой задаче требуется определить экстремум функционала  при наличии своеобразного дополнительного условия — длина кривой должна быть постоянна, т. е. функционал
при наличии своеобразного дополнительного условия — длина кривой должна быть постоянна, т. е. функционал

сохраняет постоянное значение. Условия такого типа называются изопериметрическими. Общие методы решения задач с изопериметрическими условиями были разработаны Л. Эйлером.
Вариация и ее свойства.
Методы решения вариационных задач, т. е. задач на исследование функционалов на максимум и минимум, весьма сходны с методами исследования на максимум и минимум функций. Поэтому целесообразно напомнить кратко теорию максимума и минимума функций и параллельно ввести аналогичные понятия и доказать сходные теоремы для функционалов.
1. Переменная величина z называется функцией переменной величины х, что обозначается так:  , если каждому значению х из некоторой области изменения х соответствует значение z, т. е. имеет место соответствие: числу х соответствует число z.
Аналогично определяются и функции нескольких переменных. , если каждому значению х из некоторой области изменения х соответствует значение z, т. е. имеет место соответствие: числу х соответствует число z.
Аналогично определяются и функции нескольких переменных.
| 1. Переменная величина v называется функционалом, завися-
зависящим от функции  , что обозначается так: , что обозначается так: 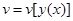 , если каждой функции , если каждой функции  из некоторого класса функций из некоторого класса функций  соответствует значение соответствует значение  , т. е. имеет место соответствие: функции , т. е. имеет место соответствие: функции  соответствует число соответствует число  . Аналогично определяются и функционалы, зависящие от нескольких функций, и функционалы, зависящие от функций нескольких независимых переменных. . Аналогично определяются и функционалы, зависящие от нескольких функций, и функционалы, зависящие от функций нескольких независимых переменных.
|
2. Приращением  аргумента х функции аргумента х функции  называется разность между двумя значениями этой переменной называется разность между двумя значениями этой переменной  .
Если х — независимое переменное, то дифференциал х совпадает с приращением .
Если х — независимое переменное, то дифференциал х совпадает с приращением  . .
| 2. Приращением или вариацией 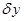 аргумента аргумента  функционала функционала 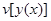 называется разность между двумя функциями называется разность между двумя функциями  . При этом предполагается, что . При этом предполагается, что  меняется произвольно в некотором классе функций. меняется произвольно в некотором классе функций.
|
3. Функция  непрерывной, если малому изменению х соответствует малое изменение функции непрерывной, если малому изменению х соответствует малое изменение функции  . .
| 3. Функционал 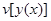 называется непрерывным, если малому изменению называется непрерывным, если малому изменению  соответствует малое изменение функционала соответствует малое изменение функционала 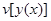 . .
|
Последнее определение нуждается в уточнении и разъяснении, так как сейчас же возникает вопрос, какие изменения функции  , являющейся аргументом функционала, называются малыми или, что то же самое, какие кривые
, являющейся аргументом функционала, называются малыми или, что то же самое, какие кривые  и
и  считаются мало отличающимися или близкими.
считаются мало отличающимися или близкими.
Можно считать близкими функции  и
и  в том случае, если модуль их разности
в том случае, если модуль их разности  мал для всех значений х, для которых задаются функции
мал для всех значений х, для которых задаются функции  и
и  , т. е. считать близкими кривые, близкие по ординатам.
, т. е. считать близкими кривые, близкие по ординатам.
Однако при таком определении близости кривых часто встречающиеся в приложениях функционалы вида

из-за наличия в подынтегральной функции аргумента у' лишь в исключительных случаях будут непрерывными. Поэтому во многих случаях более естественно считать близкими только те кривые, которые близки по ординатам и по направлениям касательных в соответствующих точках, т. е. требовать, чтобы для близких кривых не только модуль разности  был бы мал, но, кроме того, был бы мал и модуль разности
был бы мал, но, кроме того, был бы мал и модуль разности  .
.
Иногда же оказывается необходимым считать близкими только те функции, для которых малы модули каждой из разностей:
 ,
,  ,…,
,…, 
В связи с этим приходится ввести следующие определения близости кривых  и
и  .
.
Кривые  и
и  близки в смысле близости нулевого порядка, если модуль разности
близки в смысле близости нулевого порядка, если модуль разности  мал.
мал.
Кривые  и
и  близки в смысле близости первого порядка, если модули разностей
близки в смысле близости первого порядка, если модули разностей  и
и  малы.
малы.
Кривые  и
и  близки в смысле близости к -го порядка, если модули разностей
близки в смысле близости к -го порядка, если модули разностей
 ,
,  ,…,
,…, 
малы.
 На рис. 6.1 изображены кривые, близкие в смысле близости нулевого порядка, но не близкие в смысле близости первого порядка, так как ординаты у них близки, а направления касательных не близки. На рис. 6.2 изображены кривые, близкие в смысле близости первого
На рис. 6.1 изображены кривые, близкие в смысле близости нулевого порядка, но не близкие в смысле близости первого порядка, так как ординаты у них близки, а направления касательных не близки. На рис. 6.2 изображены кривые, близкие в смысле близости первого
порядка.
Из этих определений следует, что если кривые близки в смысле близости к -го порядка, то они тем более близки в смысле близости любого меньшего порядка.
Теперь мы можем уточнить понятие непрерывности функционала.
3`.Функция  непрерывна при непрерывна при  , если для любого положительного , если для любого положительного 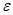 можно подобрать можно подобрать  такое, что такое, что 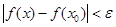 , при , при  . При этом подразумевается, что х принимает значения, в которых функция . При этом подразумевается, что х принимает значения, в которых функция  определена. определена.
| 3`.Функционал 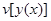 непрерывен при непрерывен при  в смысле близости к -го порядка, если для любого положительного в смысле близости к -го порядка, если для любого положительного 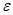 можно подобрать можно подобрать  такое, что такое, что  , при , при

 ….
….
 При этом подразумевается, что функция
При этом подразумевается, что функция  берется из класса функций, на котором функционал берется из класса функций, на котором функционал 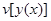 определен. определен.
|
4. Линейной функцией называется функция  , удовлетворяющая следующим условиям: , удовлетворяющая следующим условиям:

 Линейная функция одной переменной имеет вид:
Линейная функция одной переменной имеет вид:

| 4. Линейным функционалом называется
функционал  , удовлетворяющая следующим условиям: , удовлетворяющая следующим условиям:
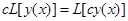
 Примером линейного функционала является:
Примером линейного функционала является:

|
5. Если приращение функции
 можно представить в виде
можно представить в виде
 где
где  не зависит от не зависит от  , а , а  , при , при  , то функция называется дифференцируемой, а линейная по отношению к , то функция называется дифференцируемой, а линейная по отношению к  часть приращения называется дифференциалом функции и обозначается часть приращения называется дифференциалом функции и обозначается 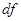

| 5. Если приращение функционала
 можно представить в виде
можно представить в виде
 где
где  - линейны по отношению к - линейны по отношению к 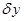 функционал, а функционал, а  - максимальное значение - максимальное значение  и и 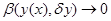 , при , при  , то линейная по отношению к , то линейная по отношению к 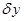 часть приращения функционала, т.е. часть приращения функционала, т.е.  , называется вариацией функционала и обозначается , называется вариацией функционала и обозначается 
|
Итак, вариация функционала — это главная, линейная по отношению к 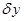 , часть приращения функционала.
, часть приращения функционала.
При исследовании функционалов вариация играет такую же роль, какую играет дифференциал при исследовании функций.
Можно дать и другое, почти эквивалентное, определение дифференциала функции и вариации функционала. Рассмотрим значение функции  при фиксированном
при фиксированном  х и
х и  и изменяющихся значениях параметра
и изменяющихся значениях параметра 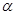 . При
. При  получим приращенное значение функции
получим приращенное значение функции  , при
, при  получим исходное значение функции
получим исходное значение функции  . Нетрудно проверить, что производная от
. Нетрудно проверить, что производная от  по
по 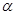 при
при  равна дифференциалу функции
равна дифференциалу функции  в точке
в точке  . Действительно, по правилу дифференцирования сложной функции
. Действительно, по правилу дифференцирования сложной функции

Точно так же для функции нескольких переменных.
И для функционалов вида 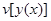 или более сложных, зависящих от нескольких неизвестных функций или от функций нескольких переменных, можно определить вариацию как производную от функционала
или более сложных, зависящих от нескольких неизвестных функций или от функций нескольких переменных, можно определить вариацию как производную от функционала  по
по 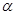 при
при  .
.
Итак, если существует вариация в смысле главной линейной части приращения функционала, то существует и вариация в смысле производной по параметру при начальном значении параметра, и оба эти определения эквивалентны.
Второе определение вариации несколько шире первого, так как существуют примеры функционалов, из приращения которых нельзя выделить главной линейной части, но вариация в смысле второго определения существует.
6. Дифференциал функции  равен равен

| 6. Вариация функционала 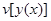 равна равна

|
Определение. Функционал 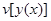 достигает на кривой
достигает на кривой  максимума, если значения функционала
максимума, если значения функционала 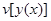 на любой близкой к
на любой близкой к  кривой не больше, чем
кривой не больше, чем  , то есть
, то есть  .
.
Если  , причем
, причем  только при
только при  , то говорят, что на кривой
, то говорят, что на кривой  достигается строгий максимум. Аналогично определяется кривая
достигается строгий максимум. Аналогично определяется кривая  , на которой реализуется минимум. В этом случае
, на которой реализуется минимум. В этом случае  для всех кривых, близких к кривой
для всех кривых, близких к кривой  .
.
7. Теорема.Если дифференцируемая функция  достигает максимума или минимума во внутренней точке достигает максимума или минимума во внутренней точке  области определения функции, то в этой точке области определения функции, то в этой точке

| 7. Теорема. Если функционал 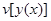 , имеющий вариацию, достигает максимума или минимума при , имеющий вариацию, достигает максимума или минимума при  , где , где  - внутренняя точка области определения функционала, то при - внутренняя точка области определения функционала, то при  , ,
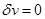
|
Итак, на кривых, на которых достигается экстремум функционала, его вариация равна нулю.
Понятие экстремума функционала нуждается в уточнении. Говоря о максимуме или минимуме, точнее, об относительном максимуме или минимуме, мы имели в виду наибольшее или наименьшее значение функционала только по отношению к значениям функционала на близких кривых. Но, как было указано выше, близость кривых может быть понимаема различно, поэтому в определении максимума или минимума надо указывать, какого порядка близость имеется в виду.
Если функционал 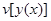 достигает на кривой
достигает на кривой  максимума или минимума по отношению ко всем кривым, для которых модуль разности
максимума или минимума по отношению ко всем кривым, для которых модуль разности  мал, т. е. по отношению к кривым, близким к
мал, т. е. по отношению к кривым, близким к  в смысле близости нулевого порядка, то максимум или минимум называется сильным.
в смысле близости нулевого порядка, то максимум или минимум называется сильным.
Если же функционал 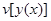 достигает на кривой
достигает на кривой  максимума или минимума лишь по отношению к кривым
максимума или минимума лишь по отношению к кривым  , близким к
, близким к  в смысле близости первого порядка, т. е. по отношению к кривым, близким к
в смысле близости первого порядка, т. е. по отношению к кривым, близким к  не только по ординатам, но и по направлениям касательных, то максимум или минимум называется слабым.
не только по ординатам, но и по направлениям касательных, то максимум или минимум называется слабым.
Очевидно, что если на кривой  достигается сильный максимум (или минимум), то подавно достигается и слабый, так как если кривая близка к
достигается сильный максимум (или минимум), то подавно достигается и слабый, так как если кривая близка к  в смысле близости первого порядка, то она близка и в смысле близости нулевого порядка. Однако возможно, что на кривой
в смысле близости первого порядка, то она близка и в смысле близости нулевого порядка. Однако возможно, что на кривой  достигается слабый максимум (минимум) и в то же время не достигается сильный максимум (минимум), т. е. среди кривых
достигается слабый максимум (минимум) и в то же время не достигается сильный максимум (минимум), т. е. среди кривых  , близких к
, близких к  как по ординатам, так и по направлению касательных, может не быть таких, для которых
как по ординатам, так и по направлению касательных, может не быть таких, для которых  (в случае минимума
(в случае минимума  ), а среди кривых
), а среди кривых  , близких только по ординатам, но уже не близких по направлению касательных, могут найтись и такие, для которых
, близких только по ординатам, но уже не близких по направлению касательных, могут найтись и такие, для которых  (в случае минимума
(в случае минимума  ).
).
Заметим еще, что если на кривой  достигается экстремум, то не только
достигается экстремум, то не только  , но и
, но и  , где
, где  — любое семейство допустимых кривых, причем при
— любое семейство допустимых кривых, причем при  и при
и при  функция
функция  должна соответственно превращаться в
должна соответственно превращаться в  и
и  . Действительно,
. Действительно,  является функцией
является функцией 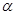 , так как задание
, так как задание 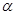 определяет кривую семейства
определяет кривую семейства  , а значит, определяет и значение функционала
, а значит, определяет и значение функционала  .
.
Эта функция, по предположению, достигает экстремума при  , следовательно, производная этой функции обращается в нуль при
, следовательно, производная этой функции обращается в нуль при  .
.
Итак,  , однако эта производная, вообще говоря, уже не будет совпадать с вариацией функционала, но будет, как показано выше, обращаться в нуль одновременно с
, однако эта производная, вообще говоря, уже не будет совпадать с вариацией функционала, но будет, как показано выше, обращаться в нуль одновременно с  на кривых, реализующих экстремум функционала.
на кривых, реализующих экстремум функционала.
Все определения этого параграфа и основная теорема почти без всякого изменения переносятся на функционалы, зависящие от нескольких неизвестных функций

или зависящие от одной или нескольких функций многих переменных
 ,
, 
Например, вариация  функционала
функционала  , может быть определена или как главная линейная по отношению к
, может быть определена или как главная линейная по отношению к  часть приращения
часть приращения
 ,
,
или как производная по параметру при начальном значении параметра
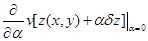
причем если при  функционал
функционал  достигает экстремума, то при
достигает экстремума, то при  вариация
вариация 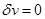 , так как
, так как  является функцией
является функцией 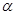 , которая при
, которая при  , по предположению, достигает экстремума и, следовательно, производная от этой функции по
, по предположению, достигает экстремума и, следовательно, производная от этой функции по 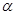 при
при  обращается в нуль,
обращается в нуль,  или
или 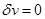 .
.
Уравнение Эйлера.
 Исследуем на экстремум функционал
Исследуем на экстремум функционал
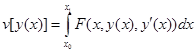 (1)
(1)
причем граничные точки допустимых кривых закреплены:  и
и  (рис. 6.3). Функцию F(x, у, у') будем считать трижды дифференцируемой.
(рис. 6.3). Функцию F(x, у, у') будем считать трижды дифференцируемой.
Мы уже знаем, что необходимым условием экстремума является обращение в нуль вариации функционала. Покажем теперь, как применяется эта основная теорема к рассматриваемому функционалу, причем мы еще раз повторим предыдущее рассуждение применительно к функционалу (1). Предположим, что экстремум достигается на дважды дифференцируемой кривой у = у (х) (требуя лишь существования производных первого порядка у допустимых кривых, можно иным методом доказать, что у кривой, реализующей экстремум, существует и вторая производная).
Возьмем какую-нибудь близкую к  допустимую кривую
допустимую кривую 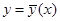 и включим эти кривые в однопараметрическое семейство кривых
и включим эти кривые в однопараметрическое семейство кривых

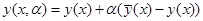
при  получим
получим  , в противном случае
, в противном случае 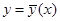 (рис. 6.4). Как мы уже знаем, разность
(рис. 6.4). Как мы уже знаем, разность  называется вариацией функции у(х).
называется вариацией функции у(х).
Вариация 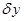 в вариационных задачах играет роль, аналогичную роли приращения независимого переменного в задачах на исследование экстремумов функций
в вариационных задачах играет роль, аналогичную роли приращения независимого переменного в задачах на исследование экстремумов функций  . Вариация функции
. Вариация функции  является функцией х. Эту функцию можно дифференцировать один или несколько раз, причем производная вариации равна вариации производной.
является функцией х. Эту функцию можно дифференцировать один или несколько раз, причем производная вариации равна вариации производной.
Итак, рассмотрим семейство  ,
,  , содержащее при
, содержащее при  кривую, на которой достигается экстремум, а при
кривую, на которой достигается экстремум, а при  — некоторую близкую допустимую кривую — так называемую кривую сравнения.
— некоторую близкую допустимую кривую — так называемую кривую сравнения.
Если рассматривать значения функционала
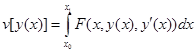
только на кривых семейства  , то функционал превращается в функцию
, то функционал превращается в функцию 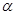 :
:

так как значение параметра 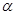 определяет кривую семейства
определяет кривую семейства  и тем самым определяет и значение функционала
и тем самым определяет и значение функционала  . Эта функция
. Эта функция  достигает своего экстремума при
достигает своего экстремума при  , так как при
, так как при  получаем
получаем  , и функционал, по предположению, достигает экстремума по сравнению с любой близкой допустимой кривой и, в частности, по отношению к близким кривым семейства
, и функционал, по предположению, достигает экстремума по сравнению с любой близкой допустимой кривой и, в частности, по отношению к близким кривым семейства  . Необходимым условием экстремума функции
. Необходимым условием экстремума функции  при
при  , как известно, является обращение в нуль ее производной при
, как известно, является обращение в нуль ее производной при  :
:

Так как

то
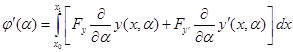

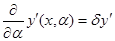
Тогда при  получаем:
получаем:

Как мы уже знаем, 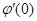 называется вариацией функционала и обозначается
называется вариацией функционала и обозначается  . Необходимое условие экстремума функционала
. Необходимое условие экстремума функционала  заключается в обращении в нуль его вариации:
заключается в обращении в нуль его вариации: 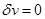 . Для функционала
. Для функционала
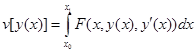
Это условие имеет вид:

Интегрируем второе слагаемое по частям, получаем:

Первое слагаемое в силу того что концы закреплены обращается в нуль.
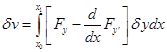
Таким образом, необходимое условие экстремума приобретает вид:

причем первый множитель на кривой  , реализующей экстремум, является заданной непрерывной функцией, а второй множитель, ввиду произвола в выборе кривой сравнения, является произвольной функцией, удовлетворяющей лишь некоторым весьма общим условиям, а именно: функция
, реализующей экстремум, является заданной непрерывной функцией, а второй множитель, ввиду произвола в выборе кривой сравнения, является произвольной функцией, удовлетворяющей лишь некоторым весьма общим условиям, а именно: функция 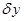 в граничных точках обращается в нуль, непрерывна и дифференцируема один или несколько раз.
в граничных точках обращается в нуль, непрерывна и дифференцируема один или несколько раз. 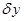 или
или 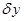 и
и  малы по абсолютной величине.
малы по абсолютной величине.
Для упрощения полученного условия воспользуемся следующей леммой:
Основная лемма вариационного исчисления. Если для каждой непрерывной функции 

где функция Ф(х) непрерывна на отрезке  , то
, то

на том же отрезке.
Для нашего случая все условия леммы выполнены: на кривой, реализующей экстремум, множитель  является непрерывной функцией, а вариация
является непрерывной функцией, а вариация 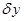 является произвольной функцией, на которую наложены лишь предусмотренные в основной лемме ограничения общего характера, следовательно,
является произвольной функцией, на которую наложены лишь предусмотренные в основной лемме ограничения общего характера, следовательно, 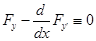 на кривой
на кривой  , реализующей экстремум рассматриваемого функционала, т. е.
, реализующей экстремум рассматриваемого функционала, т. е.  является решением дифференциального уравнения второго порядка
является решением дифференциального уравнения второго порядка

или в развернутом виде

Это уравнение называется уравнением Эйлера (оно впервые было им опубликовано в 1744 году). Интегральные кривые уравнения Эйлера  называются экстремалями. Только на экстремалях может достигаться экстремум функционала
называются экстремалями. Только на экстремалях может достигаться экстремум функционала
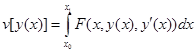
Для нахождения кривой, реализующей экстремум этого функционала, интегрируем уравнение Эйлера и определяем обе произвольные постоянные, входящие в общее решение этого уравнения, из условий на границе. Только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функционала. Однако для того чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума.
Заметим, что во многих вариационных задачах существование решения очевидно из физического или геометрического смысла задачи, и если решение уравнения Эйлера, удовлетворяющее граничным условиям, единственно, то эта единственная экстремаль и будет решением рассматриваемой вариационной задачи.
Пример 1. На каких кривых может достигать экстремума функционал:
 ,
, 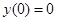 ,
, 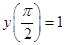
Уравнение Эйлера имеет вид 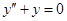 . Его решение, учитывая граничные условия:
. Его решение, учитывая граничные условия:

Пример 2. На каких кривых может достигать экстремума функционал:
 ,
, 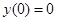 ,
, 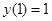
Уравнение Эйлера  , решение
, решение 
В этих двух примерах уравнение Эйлера легко интегрировалось, но так бывает далеко не всегда, так как дифференциальные уравнения второго порядка интегрируются в конечном виде лишь в исключительных случаях. Рассмотрим некоторые простейшие случаи интегрируемости уравнения Эйлера.
1) F зависит лишь от  .
.

В этом случае 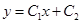
Пример 3. Длина дуги кривой:

имеет экстремали 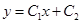
Пример 4. Время, затрачиваемое на перемещение из одной точки в другую:

так же имеет экстремалями прямые линии.
2) F зависит лишь от x и  .
.
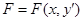
Уравнение Эйлера  , следовательно
, следовательно 
3) F зависит лишь от  и
и  .
.

Уравнение Эйлера имеет вид  . Если умножить это уравнение на
. Если умножить это уравнение на  , то
, то  . Следовательно, уравнение Эйлера имеет первый интеграл:
. Следовательно, уравнение Эйлера имеет первый интеграл:

Пример 5. Задача о наименьшей поверхности вращения:

После упрощений получаем

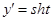 , тогда
, тогда  .
. 
После исключения параметра t будем иметь:

§ 1.3 Функционалы вида 
Для получения необходимых условий экстремума функционала  более общего вида
более общего вида

при заданных граничных значениях всех функций

будем варьировать лишь одну из функций
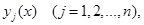
оставляя все остальные функции неизменными. При этом функционал  превратится в функционал, зависящий лишь от одной варьируемой функции, например от
превратится в функционал, зависящий лишь от одной варьируемой функции, например от  ,
,
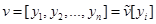
рассмотренного в § 2 вида, и, следовательно, функция, реализующая экстремум, должна удовлетворять уравнению Эйлера
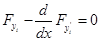
Так как это рассуждение применимо к любой функции 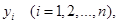 то мы получим систему дифференциальных уравнений второго порядка
то мы получим систему дифференциальных уравнений второго порядка

определяющих, вообще говоря, 2n-параметрическое семейство интегральных кривых в пространстве  — семейство экстремалей данной вариационной задачи.
— семейство экстремалей данной вариационной задачи.
Если, в частности, функционал зависит лишь от двух функций
у(х) и z(x):


т. е. определяется выбором пространственной кривой  (рис. 6.11), то, варьируя только
(рис. 6.11), то, варьируя только  и фиксируя
и фиксируя  , Рис. 6.11.
, Рис. 6.11.

мы изменяем нашу кривую так, что ее проекция на плоскости  не изменяется, т. е. кривая все время остается на проектирующем цилиндре
не изменяется, т. е. кривая все время остается на проектирующем цилиндре 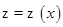 (рис. 6.12).
(рис. 6.12).

Аналогично, фиксируя  и варьируя
и варьируя  , мы варьируем кривую так, что она все время лежит на проектирующем цилиндре
, мы варьируем кривую так, что она все время лежит на проектирующем цилиндре  При этом получаем систему двух уравнений Эйлера:
При этом получаем систему двух уравнений Эйлера:
 .
.
Пример 1. Найти экстремали функционала

Система дифференциальных уравнений Эйлера имеет вид

Исключая одну из неизвестных функций, например z, получаем 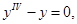
Интегрируя это линейное уравнение с постоянными коэффициентами, будем
иметь;

Используя граничные условия, находим:

следовательно,  .
.
Пример 2. Найти экстремали функционала

Система уравнений Эйлера имеет вид

откуда, считая,  получим:
получим:  и
и  или
или  — семейство прямых линий в пространстве.
— семейство прямых линий в пространстве.
Пример 3. Найти дифференциальные уравнения линий распространения света в оптически неоднородной среде, в которой скорость распространения света равна  .
.
Согласно принципу Ферми свет распространяется из одной точки  в другую
в другую  пo кривой, для которой время Т прохождения света будет наименьшим. Если уравнение искомой кривой
пo кривой, для которой время Т прохождения света будет наименьшим. Если уравнение искомой кривой 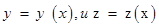 , то
, то
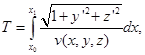
Система уравнений Эйлера для этого функционала

и будет системой, определяющей линии распространения света.
Не нашли, что искали? Воспользуйтесь поиском: