Тема 1. Матриці та визначники

Варіант 1

Задані дві матриці: 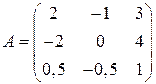і .

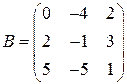1) Виконати дії: а) множення матриці на число ;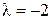

б) додавання та віднімання двох матриць ;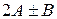

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 2

Задані дві матриці: 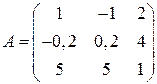і .

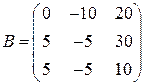1) Виконати дії: а) множення матриці на число ;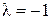

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .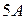

3) Знайти обернену матрицю до матриці .

Варіант 3

Задані дві матриці: 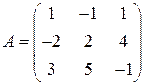і .

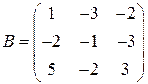1) Виконати дії: а) множення матриці на число ;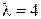

б) додавання та віднімання двох матриць ;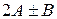

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 4

Задані дві матриці: 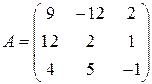і .

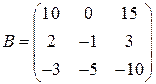1) Виконати дії: а) множення матриці на число ;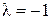

б) додавання та віднімання двох матриць ;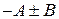

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 5

Задані дві матриці: 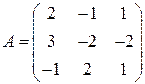і .

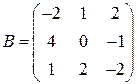1) Виконати дії: а) множення матриці на число ;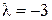

б) додавання та віднімання двох матриць ;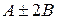

в) множення .

2) Обчислити визначник матриці .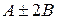

3) Знайти обернену матрицю до матриці .

Варіант 6

Задані дві матриці: 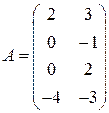і .

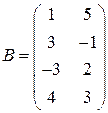1) Виконати дії: а) множення матриці на число ;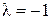

б) додавання та віднімання двох матриць ;

в) множення .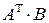

2) Обчислити визначник матриці .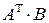

3) Знайти обернену матрицю до матриці .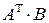

Варіант 7

Задані дві матриці: 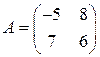і .

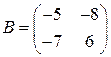1) Виконати дії: а) множення матриці на число ;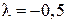

б) додавання та віднімання двох матриць ;

в) множення та .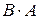

2) Обчислити визначник отриманої матриці .

3) Знайти обернену матрицю до матриці .

Варіант 8

Задані дві матриці: 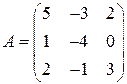і .

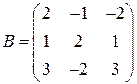1) Виконати дії: а) множення матриці на число ;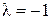

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник отриманої матриці .

3) Знайти обернену матрицю до матриці .

Варіант 9

Задані дві матриці: 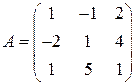і .

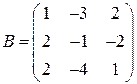1) Виконати дії: а) множення матриці на число ;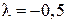

б) додавання та віднімання двох матриць ;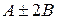

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 10

Задані дві матриці: і .

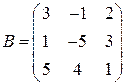1) Виконати дії: а) множення матриці на число ;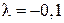

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 11

Задані дві матриці: 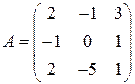і .

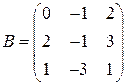1) Виконати дії: а) множення матриці на число ;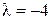

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 12

Задані дві матриці: 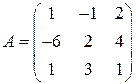і .

1) Виконати дії: а) множення матриці на число ;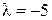

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 13

Задані дві матриці: 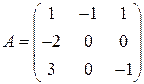і .

1) Виконати дії: а) множення матриці на число ;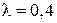

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 14

Задані дві матриці: і .

1) Виконати дії: а) множення матриці на число ;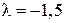

б) додавання та віднімання двох матриць ;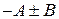

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 15

Задані дві матриці: 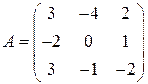і .

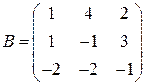1) Виконати дії: а) множення матриці на число ;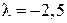

б) додавання та віднімання двох матриць ;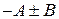

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 16

Задані дві матриці: 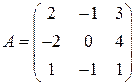і .

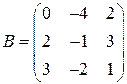1) Виконати дії: а) множення матриці на число ;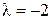

б) додавання та віднімання двох матриць ;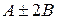

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 17

Задані дві матриці: 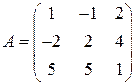і .

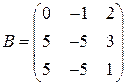1) Виконати дії: а) множення матриці на число ;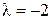

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .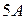

3) Знайти обернену матрицю до матриці .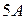

Варіант 18

Задані дві матриці: 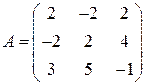і .

1) Виконати дії: а) множення матриці на число ;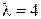

б) додавання та віднімання двох матриць ;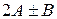

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 19

Задані дві матриці: 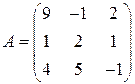і .

1) Виконати дії: а) множення матриці на число ;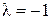

б) додавання та віднімання двох матриць ;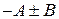

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 20

Задані дві матриці: 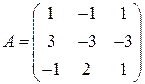і .

1) Виконати дії: а) множення матриці на число ;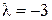

б) додавання та віднімання двох матриць ;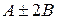

в) множення .

2) Обчислити визначник матриці .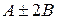

3) Знайти обернену матрицю до матриці .

Варіант 21

Задані дві матриці: 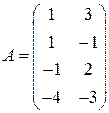і .

1) Виконати дії: а) множення матриці на число ;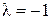

б) додавання та віднімання двох матриць ;

в) множення .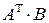

2) Обчислити визначник матриці .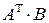

3) Знайти обернену матрицю до матриці .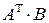

Варіант 22

Задані дві матриці: і .

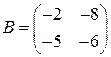1) Виконати дії: а) множення матриці на число ;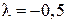

б) додавання та віднімання двох матриць ;

в) множення та .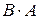

2) Обчислити визначник отриманої матриці .

3) Знайти обернену матрицю до матриці .

Варіант 23

Задані дві матриці: 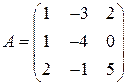і .

1) Виконати дії: а) множення матриці на число ;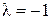

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник отриманої матриці .

3) Знайти обернену матрицю до матриці .

Варіант 24

Задані дві матриці: 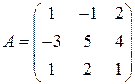і .

1) Виконати дії: а) множення матриці на число ;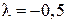

б) додавання та віднімання двох матриць ;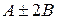

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 25

Задані дві матриці: і .

1) Виконати дії: а) множення матриці на число ;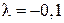

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 26

Задані дві матриці: 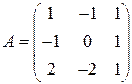і .

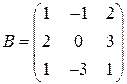1) Виконати дії: а) множення матриці на число ;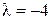

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 27

Задані дві матриці: 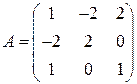і .

1) Виконати дії: а) множення матриці на число ;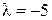

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 28

Задані дві матриці: 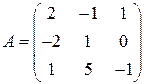і .

1) Виконати дії: а) множення матриці на число ;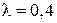

б) додавання та віднімання двох матриць ;

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 29

Задані дві матриці: 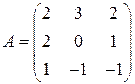і .

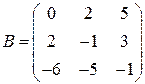1) Виконати дії: а) множення матриці на число ;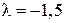

б) додавання та віднімання двох матриць ;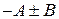

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Варіант 30

Задані дві матриці: і .

1) Виконати дії: а) множення матриці на число ;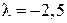

б) додавання та віднімання двох матриць ;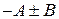

в) множення .

2) Обчислити визначник матриці .

3) Знайти обернену матрицю до матриці .

Тема 2. Ранг матриці. Системи лінійних рівнянь

Варіант 1

Завдання 1. Використовуючи елементарні перетворення, встановити ранг матриці

.

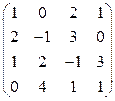Завдання 2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці).

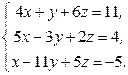
Варіант 2

Завдання 1. Використовуючи елементарні перетворення, встановити ранг матриці

.

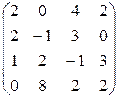Завдання 2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці).

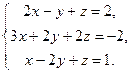
Варіант 3

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

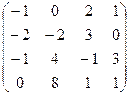Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 4

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

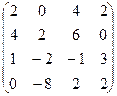
Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці).

Варіант 5

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

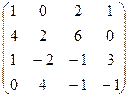Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

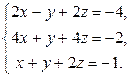
Варіант 6

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці).

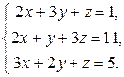
Варіант 7

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

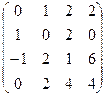Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

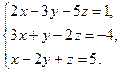
Варіант 8

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

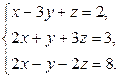
Варіант 9

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

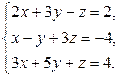
Варіант 10

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

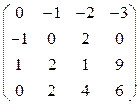Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 11

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

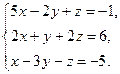
Варіант 12

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

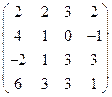Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

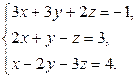
Варіант 13

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

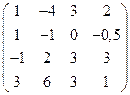Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 14

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

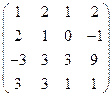Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

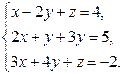
Варіант 15

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

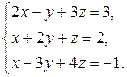
Варіант 16

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

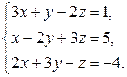
Варіант 17

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

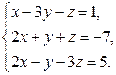
Варіант 18

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

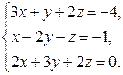
Варіант 19

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

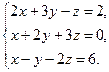
Варіант 20

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

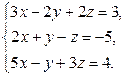
Варіант 21

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 22

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

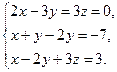
Варіант 23

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 24

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

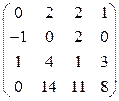Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

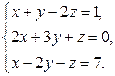
Варіант 25

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

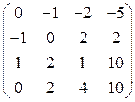Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

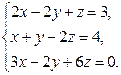
Варіант 26

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

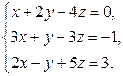
Варіант 27

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

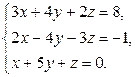
Варіант 28

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

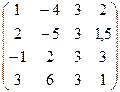Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Варіант 29

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

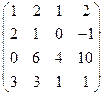Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

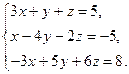
Варіант 30

Завдання1. Використовуючи елементарні перетворення, встановити ранг матриці

.

Завдання2. Розв’язати системи рівнянь: а) методом Гаусса; б) за формулами Крамера; в) матричним методом (з допомогою оберненої матриці)

Не нашли, что искали? Воспользуйтесь поиском: