Тема 5. Аналітична геометрія на площині

Варіант 1

1. Дано вершини трикутника: А(3; 2), В(-1; -1), С(11; -6). Визначити довжину його сторін.

2. Знайти рівняння прямих, що належать до пучка: , і перпендикулярних до кожної з основних прямих пучка.

3. Скласти рівняння гіперболи, осі якої збігаються з осями координат, знаючи, що: а) віддаль між вершинами дорівнює 8, а віддаль між фокусами 10; б) дійсна піввісь дорівнює 5 і вершини поділяють віддалі між центром і фокусами пополам.

Варіант 2

1. Довести, що трикутник з вершинами А(0; 0), В(3; 1), С(1; 7) прямокутний.

2. Знайти траєкторію точки, яка при своєму русі залишається у півтора рази далі від точки F(0; 6), ніж від прямої .

3. Дано рівняння сторін трикутника: , і . Знайти всередині трикутника таку точку, щоб прямі, які з’єднують її з вершинами трикутника, розбивали його на три рівновеликі трикутники.

Варіант 3

1. Визначити ординату точки М, знаючи, що абсциса її дорівнює 7, а віддаль до точки А(-1; 5) дорівнює 10.

2. Задано дві точки А(-1; 3) і В(5; -3). Скласти рівняння прямої лінії, перпендикулярної до відрізка АВ і яка поділяє його у відношенні .

3. Віддалі одного з фокусів еліпса до кінців його великої осі відповідно дорівнюють 7 і 1. Скласти рівняння цього еліпса.

Варіант 4

1. На осі ординат знайти точку, яка віддалена від точки А(4; -6) на 5 одиниць.

2. Написати рівняння прямої, яка проходить через початок координат і

а) паралельна до прямої ;

б) нахилена під кутом 60⁰ до прямої .

3. Знайти рівняння кола, якщо відомі координати кінців одного з діаметрів його АВ: А(1; 4) і В(-3; 2).

Варіант 5

1. На бісектрисах координатного кута знайти точки, віддаль яких від точки М(-2; 0) дорівнює 10.

2. Промінь світла напрямлений по прямій , дійшовши до осі абсцис, він від неї відбився. Визначити точку зустрічі променя з віссю і рівняння відбитого променя.

3. Скласти найпростіше рівняння еліпса, знаючи, що: а) півосі його відповідно дорівнюють 4 і 2; б) віддаль між фокусами дорівнює 6 і велика піввісь 5.

Варіант 6

1. Пряма лінія проходить через точку А(3; 1) і утворює з віссю ОХ кут 45⁰. На цій прямій знайти точку, ордината якої дорівнює 4.

2. Написати рівняння бісектрис кутів, утворених прямими: і .

3. Струмінь води, який викидається фонтаном, приймає форму параболи, параметр якої . Визначити висоту струменя, якщо відомо, що вода падає у басейн на віддалі 2м від місця виходу.

Варіант 7

1. Знайти центр правильного шестикутника, знаючи дві сусідні його вершини: А(2; 0) і В(5; ).

2. Через точку перетину прямих і провести пряму, яка крім того, проходить через початок координат.

3. Скласти рівняння гіперболи, яка має спільні фокуси з еліпсом , при умові, що ексцентриситет дорівнює 1,25.

Варіант 8

1. Знаючи дві протилежні вершини ромба А(8; -3), С(10; 11) і довжину сторони АВ=10, визначити координати інших вершин ромба.

2. Скласти рівняння сторін трикутника, знаючи одну з його вершин А(-4; 2), і рівняння двох медіан: .

3. Як перетвориться рівняння кола , якщо перенести початок координат у його центр.

Варіант 9

1. Перевірити, що чотирикутник з вершинами А(1; 3), В(4; 7), С(2; 8) і

D(-1; 4) – паралелограм і обчислити його висоту, взявши АВ за основу.

2. Дано трикутник з вершинами: А(1; 2), В(3; 7), С(5; -13). Обчислити довжину перпендикуляра, опущеного з вершини В на медіану, проведену з вершини А.

3. Скласти рівняння кола, яке дотикається осі ОХ в точці (5; 0) і відтинає від осі ОУ хорду довжиною 10 одиниць.

Варіант 10

1. Обчислити площу трикутника з вершинами А(4; 2), В(9; 4), С(7; 6).

2. Через точку М(3; 2) провести пряму так, щоб її відрізок, замкнений між осями координат, поділявся в даній точці пополам.

3. Через фокус 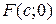еліпса проведено хорду, перпендикулярну до великої осі. Знайти довжину цієї хорди.

Варіант 11

1. Центр ваги однорідного стержня є в точці М(5; 1); один із кінців його співпадає з точкою А(-1; -3). Визначити положення другого кінця.

2. При якому значенні параметра прямі і 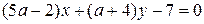будуть перпендикулярні одна до одної.

3. Дано гіперболу . Треба: а) обчислити координати фокусів та знайти ексцентриситет; б) написати рівняння асимптот.

Варіант 12

1. Визначити траєкторію точки М, яка при своєму русі залишається вдвоє ближче до точки А(1; 0), ніж до точки В(4; 0).

2. Перевірити, що чотири точки А(-2; -2), В(-3; 1), С(7; 7), D(3; 1) є вершинами трапеції і скласти рівняння середньої лінії і діагоналей трапеції.

3. Обчислити півосі гіперболи, знаючи, що віддаль між фокусами дорівнює 8 і віддаль між директрисами 6 (рівняння директрис ).

Варіант 13

1. Скласти рівняння геометричного місця точок, що знаходяться від точки А(3; 0) вдвоє ближче ніж до прямої х =12.

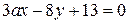2. При якому значенні параметра рівняння і рівняння зображають паралельні прямі.

3. Визначити центр і радіус кола, даного рівнянням: .

Варіант 14

1. Написати рівняння прямої, яка проходить через точку А(3; -1) і паралельна:

а) бісектрисі першого координатного кута; б) прямій .

2. Обчислити координати точки перетину перпендикулярів, поставлених до середин сторін трикутника, вершинами якого є точки: А(2; 3), В(0; -3);

С(5; -2).

3. Скласти найпростіше рівняння еліпса, знаючи, що: а) велика піввісь дорівнює 10 і ексцентриситет 0,8; б) сума півосей дорівнює8 і віддаль між фокусами 8.

Варіант 15

1. Сила Р прикладена до початку координат, і її складові на осі координат відповідно рівні 5 і -2. Записати рівняння прямої, по якій напрямлена сила.

2. Через точку перетину прямих і провести пряму, яка крім того паралельна до осі абсцис.

3. На параболі знайти точку, фокальний радіус-вектор якої дорівнює 20.

Варіант 16

1. Дано вершини трикутника: А(3; 2), В(-1; -1), С(11; -7). Визначити довжину медіани АЕ.

2. Знайти рівняння прямих, що належать до пучка: . Знайти центр пучка прямих.

3. Скласти рівняння гіперболи, осі якої збігаються з осями координат, знаючи, що: а) дійсна вісь дорівнює 6 і гіпербола проходить через точку

(9; 4); б) гіпербола проходить через точки Р (-5; 2) і .

Варіант 17

1. На осі абсцис знайти точку, яка віддалена від точки А(4; -6) на 5 одиниць.

2. Написати рівняння прямої, яка проходить через початок координат і

а) перпендикулярна до прямої ;

б) утворює кут 45⁰ з прямою .

3. Знайти рівняння кола, якщо відомі координати кінців одного з діаметрів його АВ: А(2; 4) і В(6; 8).

Варіант 18

1. Знайти радіус кола описаного навколо трикутника з вершинами А(0; 0), В(3; 0), С(0; 4).

2. Знайти траєкторію точки, яка при своєму русі залишається у два рази далі від точки F(0; 6), ніж від прямої .

3. Дано рівняння сторін трикутника: , і . Знайти точку перетину висот трикутника.

Варіант 19

1. Визначити ординату точки М, знаючи, що абсциса її дорівнює 9, а віддаль до точки А(-1; 5) дорівнює 10.

2. Задано дві точки А(-3 3) і В(6; -3). Скласти рівняння прямої лінії, перпендикулярної до відрізка АВ і яка поділяє його у відношенні .

3. Віддалі одного з фокусів еліпса до кінців його великої осі відповідно дорівнюють 6 і 4. Скласти рівняння цього еліпса.

Варіант 20

1. На бісектрисах координатного кута знайти точки, віддаль яких від точки М(-1; 0) дорівнює 1.

2. Промінь світла напрямлений по прямій , дійшовши до осі абсцис, він від неї відбився. Визначити точку зустрічі променя з віссю і рівняння відбитого променя.

3. Скласти найпростіше рівняння еліпса, знаючи, що: а) півосі його відповідно дорівнюють 5 і 1; б) віддаль між фокусами дорівнює 8 і велика піввісь 5.

Варіант 21

1. Пряма лінія проходить через точку А(2; 1) і утворює з віссю ОХ кут 45⁰. На цій прямій знайти точку, ордината якої дорівнює 8.

2. Написати рівняння бісектрис кутів, утворених прямими: і .

3. Струмінь води, який викидається фонтаном, приймає форму параболи, параметр якої . Визначити висоту струменя, якщо відомо, що вода падає у басейн на віддалі 4м від місця виходу.

Варіант 22

1. Знайти центр прямокутника і вершину D, знаючи три вершини: А(1; 0), В(5; 0) і С(5;3).

2. Через точку перетину прямих і провести пряму, яка крім того, проходить через початок координат.

3. Скласти рівняння орбіти штучного супутника Землі, якщо найвища точка орбіти над Землею 5000км, а найнижча 300км. Землю вважати кулею з радіусом 6370км.

Варіант 23

1. Знаючи три вершини ромба А(0; 0), В(10; 0) і визначити координати четвертої вершини ромба.

2. Скласти рівняння висот трикутника, знаючи рівняння його сторін: .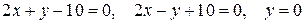

3. Записати рівняння кола у канонічному виді , знайти його центр та радіус.

Варіант 24

1. Перевірити, що чотирикутник з вершинами А(-5; 0), В(5; 0), С(10; 10) і

D(0; 10) – паралелограм і обчислити його діагоналі.

2. Дано трикутник з вершинами: А(1; 2), В(3; 7), С(5; -13). Обчислити його площу.

3. Скласти рівняння кіл, які дотикаються осі ОХ в точці (6; 0), а також дотикаються осі ОУ.

Варіант 25

1. Обчислити площу паралелограма з вершинами .

2. Через точку М(4; 2) провести пряму так, щоб її відрізок, замкнений між осями координат, поділявся в даній точці пополам.

3. Через фокус 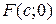еліпса проведено хорду, перпендикулярну до великої осі. Знайти довжину цієї хорди.

Варіант 26

1. Центр ваги однорідного стержня є в точці М(2; 1); один із кінців його співпадає з точкою А(-1; -3). Визначити положення другого кінця.

2. При якому значенні параметра прямі і будуть перпендикулярні одна до одної.

3. Дано гіперболу . Треба: а) обчислити координати фокусів та знайти ексцентриситет; б) написати рівняння асимптот.

Варіант 27

1. Визначити траєкторію точки М, яка при своєму русі залишається вдвоє ближче до точки А(2; 0), ніж до точки В(11; 0).

2. Перевірити, що чотири точки А(-5; 0), В(5; 0), С(1; 5), D(-1; 5) є вершинами трапеції і скласти рівняння середньої лінії і діагоналей трапеції.

3. Обчислити півосі гіперболи, знаючи, що віддаль між фокусами дорівнює 16 і віддаль між директрисами 6 (рівняння директрис ).

Варіант 28

1. Скласти рівняння прямої, що знаходяться між паралельними прямими .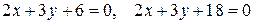

2. При якому значенні параметра рівняння і рівняння зображають перпендикулярні прямі.

3. Визначити центр і радіус кола, даного рівнянням: .

Варіант 29

1. Написати рівняння прямої, яка проходить через точку А(4; 0) і паралельна:

а) бісектрисі першого координатного кута; б) прямій .

2. Обчислити координати точки перетину перпендикулярів, поставлених до середин сторін трикутника, вершинами якого є точки: А(2; 3), В(0; -3);

С(5; -2).

3. Скласти найпростіше рівняння еліпса, знаючи, що: а) велика піввісь дорівнює 16 і ексцентриситет 0,8; б) сума півосей дорівнює 8 і віддаль між фокусами 8.

Варіант 30

1. Світловий промінь падає на поверхню води, з показником заломлення води . Кут падіння дорівнює 60⁰. Взявши точку падіння за початок координат, а нормаль в ній до поверхні води – за вісь ординат, знайти рівняння падаючого і заломленого променя (вісь абсцис – в площині променів).

2. Через точку перетину прямих і провести пряму, яка крім того паралельна до осі ординат.

3. На параболі знайти точку, фокальний радіус-вектор якої дорівнює 30.

Не нашли, что искали? Воспользуйтесь поиском: