
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 6. Аналітична геометрія в просторі
Варіант 1
1. Дано дві прямі: одна з них проходить через точки А(-3; 5; 15) і В(0; 0; 7), а друга – через точки С(2; -1; 4) і D(4; -3; 0). Дізнатися, чи перетинаються ці прямі, і якщо перетинаються, то знайти точку перетину.
В к а з і в к а. Нехай  - відношення у якому поділяється АВ спільною точкою, а
- відношення у якому поділяється АВ спільною точкою, а  - теж для СD. Тоді координати точки перетину визначаються двома способами, прирівнюючи їх, отримаємо:
- теж для СD. Тоді координати точки перетину визначаються двома способами, прирівнюючи їх, отримаємо:  . Звідси знаходимо
. Звідси знаходимо  і
і  .
.
2. Три грані тетраедра, розміщеного у другому октанті, збігаються з координатними площинами. Написати рівняння четвертої грані, знаючи довжину ребер, що її обмежують: 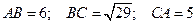 .
.
3. Обчислити віддаль між прямими: 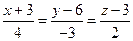 і
і  .
.
Варіант 2
1. Визначити віддаль точки А(12; -3; 4) від початку координат і від осей координат.
2. Знайти точку, симетричну з точкою (4; 3; 10) відносно прямої  .
.
3. Знайти кут між двома прямими  і
і 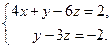
Варіант 3
1. У третьому октанті знайти точку, знаючи її віддаль від трьох осей координат:  .
.
2. Знайти відстань від точки (7; 9; 7) до прямої 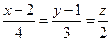 .
.
3. Знайти рівняння площини, яка проходить через паралельні прямі
 ,
,  .
.
Варіант 4
1. На осі OZ знайти точку, рівновіддалену від точок А(-4; 1; 7) і В(3; 5; -2).
2. Через пряму  провести площину, паралельну площині
провести площину, паралельну площині  .
.
3. Звести рівняння прямої 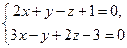 до канонічного виду.
до канонічного виду.
Варіант 5
1. На координатній площині (YOZ) знайти точку, однаково віддалену від трьох заданих точок: А(3; 1; 2), В(4; -2; -2), С(0; 5; 1).
2. Знайти точку перетину прямої  з площиною
з площиною  .
.
3. Написати рівняння площини, яка проходить через дві паралельні прямі:
 і
і 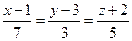 .
.
Варіант 6
1. Рухома точка, яка мала початкове положення М0(5; -1; 2), переміщається паралельно до осі ОУ. Знайти точку її зустрічі з площиною  .
.
2. Знайти проекцію точки (4; -3; 1) на площину  .
.
3. Скласти рівняння прямої, яка проходить через точки перетину площини
 з прямими
з прямими  і
і  .
.
Варіант 7
1. Знайти відстань між площинами 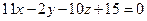 і
і  ?
?
2. При якому значенні коефіцієнта А площина  буде паралельна до прямої
буде паралельна до прямої  ?
?
3. Знайти рівняння площини, яка проходить через точки  ,
,  ,
,  .
.
Варіант 8
1. Кульова поверхня проходить через початок координат і через точки:
А(4; 0; 0), В(1; 3; 0) і С(0; 0; -4). Знайти центр і радіус кулі.
2. Скласти рівняння прямої, яка проходить через точку (1; -5; 3) і утворює з осями координат відповідно кути: 600, 450, 1200.
3. Знайти косинус кута між площинами  і
і  .
.
Варіант 9
1. Через вісь OZ провести площину, яка утворює з площиною 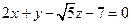 кут 600.
кут 600.
2. Визначити кут між двома прямими  і
і 
3. Задано три послідовні вершини паралелограма  ,
,  ,
,  . Знайти рівняння сторін
. Знайти рівняння сторін 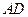 і
і  .
.
Варіант 10
1. Скласти рівняння площини, яка проходить від початку координат на віддалі 6 одиниць і відтинає на осях координат відрізки пов’язані співвідношенням:  .
.
2. Скласти рівняння прямої, яка проходить через точки перетину площини  з прямими
з прямими  і
і  .
.
3. Піраміда утворена перетином координатних площин, площиною  . Знайти її об’єм.
. Знайти її об’єм.
Варіант 11
1. Знайти площину, знаючи, що точка Р(3; -6; 2) служить основою перпендикуляра, опущеного з початку координат на цю площину.
2. Написати рівняння перпендикуляра, опущеного з точки (2; 3; 1) на пряму  .
.
3. Знайти рівняння площини, яка проходить через пряму  і перпендикулярна до площини
і перпендикулярна до площини  .
.
Варіант 12
1. Дано дві точки А(1; 3; -2) і В(7; -4; 4). Через точку В провести площину, перпендикулярну до відрізка АВ.
2. З точки (3; -2; 4) опустити перпендикуляр на площину 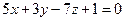 .
.
3. Вказати особливості розміщення площин відносно осей координат:
а)  ; б)
; б) 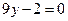 ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Варіант 13
1. Перевірити, що чотирикутник з вершинами А(5; 2; 6), В(6; 4; 4), С(4; 3; 2) і D(3; 1; 4), є квадрат.
2. Три грані тетраедра, розміщеного у другому октанті, збігаються з координатними площинами. Написати рівняння четвертої грані, знаючи довжину ребер, що її обмежують: 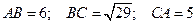 .
.
3. Обчислити віддаль між прямими: 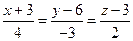 і
і  .
.
Варіант 14
1. На осях координат відкладені від початку координат відрізки, відповідно рівні 1, 2 і 3; кінці цих відрізків з’єднані прямими. Визначити площу отриманого таким чином трикутника.
2. Знайти точку, симетричну з точкою (4; 3; 10) відносно прямої  .
.
3. Знайти кут між двома прямими  і
і 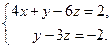
Варіант 15
1. Дано вершини трикутника А(-4; -1; 2) і В(3; 5; -6). Знайти третю вершину С, знаючи, що середина сторони АС лежить на осі ОУ, а середина сторони ВС – на площині XOZ.
2. Знайти відстань від точки (7; 9; 7) до прямої 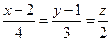 .
.
3. Знайти рівняння площини, яка проходить через паралельні прямі
 ,
,  .
.
Варіант 16
1. Знайти відношення, в якому кожна з площин координат поділяє віддаль між точками А(2; -1; 7) і В(4; 5; -2).
2. Через пряму  провести площину, паралельну площині
провести площину, паралельну площині  .
.
3. Звести рівняння прямої 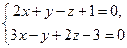 до канонічного виду.
до канонічного виду.
Варіант 17
1. Перевірити, що три точки А(1; -5; 3), В(5; -1; 7) і С(6; 0; 8) лежать на одній прямій.
2. Знайти точку перетину прямої  з площиною
з площиною  .
.
3. Написати рівняння площини, яка проходить через дві паралельні прямі:
 і
і 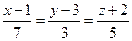 .
.
Варіант 18
1. Написати рівняння площини яка паралельна до площини(XOZ) і проходить через точку (2; -5; 3.
2. Знайти проекцію точки (4; -3; 1) на площину  .
.
3. Скласти рівняння прямої, яка проходить через точки перетину площини
 з прямими
з прямими  і
і  .
.
Варіант 19
1. Написати рівняння площини яка проходить через вісь OZ і через точку (-3; 1; -2).
2. При якому значенні коефіцієнта А площина  буде паралельна до прямої
буде паралельна до прямої  ?
?
3. Знайти рівняння площини, яка проходить через точки  ,
,  ,
,  .
.
Варіант 20
1. Написати рівняння площини яка паралельна до осі ОХ і проходить через дві точки
А(4; 0; -2) і В(5; 1; 7).
2. Скласти рівняння прямої, яка проходить через точку (1; -5; 3) і утворює з осями координат відповідно кути: 600, 450, 1200.
3. Знайти косинус кута між площинами  і
і  .
.
Варіант 21
1. Через точку Р(4; -5; 1) провести площину, яка б відтинала на осях додатні і рівні між собою відрізки.
2. Визначити кут між двома прямими  і
і 
3. Задано три послідовні вершини паралелограма  ,
,  ,
,  . Знайти рівняння сторін
. Знайти рівняння сторін 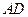 і
і  .
.
Варіант 22
1. Обчислити віддаль площини  від початку координат.
від початку координат.
2. Скласти рівняння прямої, яка проходить через точки перетину площини  з прямими
з прямими  і
і  .
.
3. Піраміда утворена перетином координатних площин, площиною  . Знайти її об’єм.
. Знайти її об’єм.
Варіант 23
1. Знайти кут між площиною 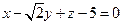 і площиною YOZ.
і площиною YOZ.
2. Написати рівняння перпендикуляра, опущеного з точки (-2; 3; 1) на пряму  .
.
3. Знайти рівняння площини, яка проходить через пряму  і перпендикулярна до площини
і перпендикулярна до площини  .
.
Варіант 24
1. Знайти точку симетричну з початком координат відносно площини  .
.
2. З точки (-1; -2; 4) опустити перпендикуляр на площину 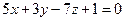 .
.
3. Вказати особливості розміщення площин відносно осей координат:
а)  ;б)
;б) 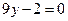 ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Варіант 25
1. Звести до нормального виду рівняння площини  .
.
2. Обчислити кут між площинами  і
і  .
.
3. Обчислити віддаль між прямими:  і
і  .
.
Варіант 26
1.Обчислити кут між площинами  і
і  .
.
2. Знайти точку перетину прямої  з площиною
з площиною  .
.
3. Знайти кут між двома прямими  і
і 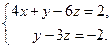
Самостійна робота
Варіант 27
1. Визначити напрямні косинуси прямої, перпендикулярної до площини  .
.
2. Знайти відстань від точки (1; 3; 7) до прямої 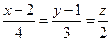 .
.
3. У площині XOZ знайти пряму, яка проходить через початок координат і перпендикулярна до прямої  .
.
Варіант 28
1. Через точку М(-5; 6; 3) проведено дві площини: одна із них проходить через вісь ОХ, друга – через вісь ОУ. Знайти кут між цими площинами.
2. Знайти точку перетину трьох площин  і
і  .
.
3. Звести рівняння прямої  до канонічного виду.
до канонічного виду.
Варіант 29
1. Перевірити, чи лежать на одній прямі три точки: (2; 0; -1), (0; 2; 4), (1; 4/3;3).
2. У пучку  знайти площину, яка відтинає рівні відрізки на осях ОХ та ОУ.
знайти площину, яка відтинає рівні відрізки на осях ОХ та ОУ.
3. Написати рівняння площини, яка проходить через дві паралельні прямі:
 і
і 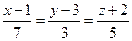 .
.
Варіант 30
1. Через лінію перетину площин  і
і 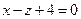 провести площину, яка утворює кут 450 з площиною
провести площину, яка утворює кут 450 з площиною  .
.
2. Записати у канонічному вигляді рівняння прямої 
3. Скласти рівняння прямої, яка проходить через точки перетину площини
 з прямими
з прямими  і
і  .
.
Не нашли, что искали? Воспользуйтесь поиском: