
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 3. Векторна алгебра
Варіант 1
1) Знайти координати точки  , якщо вектор
, якщо вектор 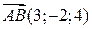 має координату
має координату
кінця вектора 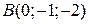 .
.
2) Знайти проекцію вектора  на вектор
на вектор 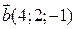 .
.
3) Знайти векторний добуток векторів  і
і  .
.
Варіант 2
1) Знайти координати точки  , якщо вектор
, якщо вектор 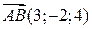 має координату початку
має координату початку 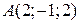 .
.
2) Знайти проекцію вектора 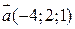 на вектор
на вектор  .
.
3) Знаючи, що 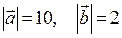 і
і 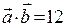 , знайти
, знайти 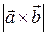 .
.
Варіант 3
1) Записати координати напрямного вектора, що йде бісектрисою другого октанта.
2) За яких умов на  і
і  вектори
вектори 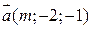 та
та 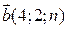 паралельні?
паралельні?
3) Знайти змішаний добуток векторів  і
і 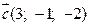 .
.
Варіант 4
1) Записати координати одиничного напрямного вектора, що йде бісектрисою третього октанта.
2) За яких умов на  і
і  вектори
вектори 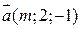 та
та 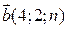 паралельні?
паралельні?
3) Знайти змішаний добуток векторів 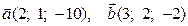 і
і  .
.
Варіант 5
1) Вектор, довжина якого дорівнює 3, має однакові координати. Знайти його.
2) Дано вектори 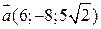 і
і  . Знайти кут, який утворює вектор
. Знайти кут, який утворює вектор 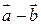 з віссю
з віссю 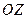 .
.
3) Вектори 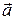 і
і  взаємно перпендикулярні. Знаючи, що
взаємно перпендикулярні. Знаючи, що  , обчислити
, обчислити 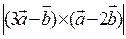 .
.
Варіант 6
1) До однієї точки прикладені дві сили  і
і  , що діють під кутом 1200, причому
, що діють під кутом 1200, причому 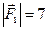 ,
,  . Знайти величину рівнодійної
. Знайти величину рівнодійної 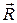 .
.
2) Дано два вектори  і
і 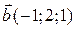 . Знайти проекції на координатні осі вектора
. Знайти проекції на координатні осі вектора 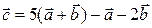 .
.
3) Задані вектори 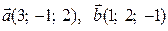 . Знайти координати вектора
. Знайти координати вектора
 .
.
Варіант 7
1) Знайти довжину вектора  , якщо
, якщо 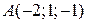 і
і  .
.
2) Обчислити площу паралелограма, побудованого на векторах 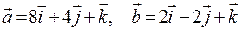 .
.
3) Задані 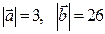 і
і  . Знайти скалярний добуток
. Знайти скалярний добуток 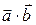 .
.
Варіант 8
1) Знайти одиничний вектор, який перпендикулярний до векторів 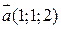 і
і 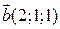 .
.
2) Дано вершини чотирикутника А(2; -1; 2), В(2; 5; 0), С(-3; 2; 1),
D(-4; -4; 3). Знайти кут між діагоналями цього чотирикутника.
3) Задані координати точок А(4; 1; 4), В(3; 4; 1), С(5; 4; 3). Знайти координати векторного добутку 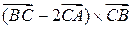 .
.
Варіант 9
1) При яких значеннях 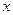 і
і 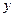 вектори
вектори  і
і 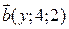 колінеарні.
колінеарні.
2) Визначити, при якому значенні t вектори 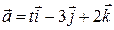 і
і 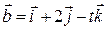 взаємно перпендикулярні.
взаємно перпендикулярні.
3) Обчислити площу трикутника з вершинами А(4; 2; 3), В(5; 1; 2),
С(6; 5; 8).
Варіант 10
1) Знайти довжину вектора  , якщо
, якщо  і
і  .
.
2) Задані вершини трикутника А(0; -1; 4), В(-3; -1; 0), С(4; -1; 1). Визначити його внутрішній кут при вершині В.
3) Вектори 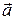 і
і  утворюють кут 1200,
утворюють кут 1200, 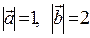 . Обчислити
. Обчислити 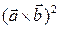 .
.
Варіант 11
1) При яких значеннях  вектори
вектори 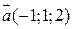 і
і 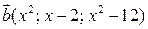 колінеарні.
колінеарні.
2) Вектор 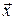 , перпендикулярний до векторів
, перпендикулярний до векторів 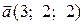 і
і 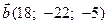 , утворює з віссю ОУ тупий кут і має довжину
, утворює з віссю ОУ тупий кут і має довжину 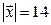 . Знайти його координати.
. Знайти його координати.
3) Обчислити мішаний добуток векторів 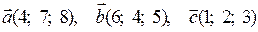 .
.
Варіант 12
1) Дано точки А(-1; 3; -3), В(4; 3; 6), С(2; 0; 3), D(4; 3; -3). Знайти проекцію вектора  на вектор
на вектор  .
.
2) Дано три вектори  і
і 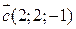 . Обчислити проекцію вектора
. Обчислити проекцію вектора 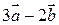 на вектор
на вектор  (
(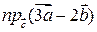 ).
).
3) Визначити, якою трійкою є трійка векторів, лівою чи правою 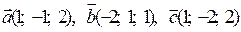 .
.
Варіант 13
1) При яких значеннях 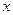 вектори
вектори  і
і 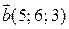 перпендикулярні.
перпендикулярні.
2) Знайти кут між ненульовими векторами 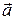 і
і  , якщо
, якщо  ,
, 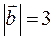 і справедлива рівність
і справедлива рівність  .
.
3) З’ясувати лінійну залежність векторів 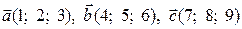 .
.
Варіант 14
1) Визначити при яких значеннях 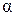 і
і 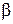 вектори
вектори  і
і 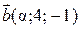 колінеарні.
колінеарні.
2) Вектори 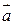 і
і 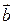 утворюють кут 300, причому
утворюють кут 300, причому 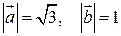 . Знайти кут між векторами
. Знайти кут між векторами 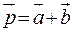 і
і  .
.
3) Знайти об’єм паралелепіпеда, побудованого на векторах  ,
, 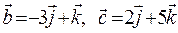 .
.
Варіант 15
1) Заданий вектор 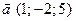 . Знайти координати вектора
. Знайти координати вектора  , який лежить у площині ХОУ і перпендикулярний до вектора
, який лежить у площині ХОУ і перпендикулярний до вектора 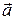 , якщо
, якщо 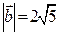 .
.
2) Знайти кут між діагоналями паралелограма, побудованого на векторах 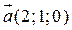 і
і 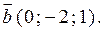
3) Знайти об’єм паралелепіпеда, побудованого на векторах 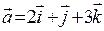 ,
,  .
.
Варіант 16
1) Знайти координати точки  , якщо вектор
, якщо вектор 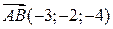 має координату кінця
має координату кінця 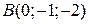 .
.
2) Знайти проекцію вектора  на вектор
на вектор 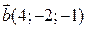 .
.
3) Знайти векторний добуток векторів 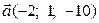 і
і 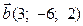 .
.
Варіант 17
1) Знайти координати точки  , якщо вектор
, якщо вектор 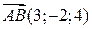 має координату початку
має координату початку 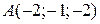 .
.
2) Знайти проекцію вектора 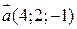 на вектор
на вектор 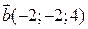 .
.
3) Знаючи, що 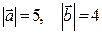 і
і  , знайти
, знайти  .
.
Варіант 18
1) Записати координати напрямного вектора, що йде бісектрисою третього октанта.
2) За яких умов на  і
і  вектори
вектори 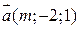 та
та 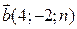 паралельні?
паралельні?
3) Знайти змішаний добуток векторів 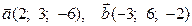 і
і 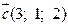 .
.
Варіант 19
1) Записати координати одиничного напрямного вектора, що йде бісектрисою п’ятого октанта.
2) За яких умов на  і
і  вектори
вектори 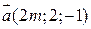 та
та 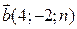 паралельні?
паралельні?
3) Знайти довжини діагоналей паралелограма побудованого на векторах 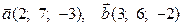 .
.
Варіант 20
1) Вектор, довжина якого дорівнює 1, має однакові координати. Знайти його.
2) Дано вектори 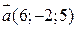 і
і  . Знайти косинус кута, який утворює вектор
. Знайти косинус кута, який утворює вектор 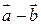 з віссю
з віссю 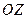 .
.
3) Вектори 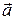 і
і  взаємно перпендикулярні. Знаючи, що
взаємно перпендикулярні. Знаючи, що  , обчислити
, обчислити 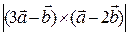 .
.
Варіант 21
1) До однієї точки прикладені дві сили  і
і  , що діють під кутом 1200, причому
, що діють під кутом 1200, причому 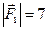 ,
,  . Знайти величину рівнодійної
. Знайти величину рівнодійної 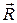 .
.
2) Дано два вектори  і
і 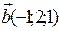 . Знайти проекції на координатні осі вектора
. Знайти проекції на координатні осі вектора 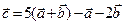 .
.
3) Задані вектори 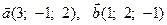 . Знайти координати вектора
. Знайти координати вектора
 .
.
Варіант 22
1) Знайти довжину вектора  , якщо
, якщо 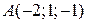 і
і  .
.
2) Обчислити площу паралелограма, побудованого на векторах 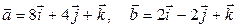 .
.
3) Задані  і
і 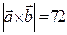 . Знайти скалярний добуток
. Знайти скалярний добуток 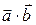 .
.
Варіант 23
1) Знайти одиничний вектор, який перпендикулярний до векторів 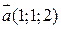 і
і 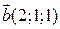 .
.
2) Дано вершини чотирикутника А(2; -1; 2), В(2; 5; 0), С(-3; 2; 1), D(-4; -4; 3). Знайти кут між діагоналями цього чотирикутника.
3) Задані координати точок А(4; 1; 4), В(3; 4; 1), С(5; 4; 3). Знайти координати векторного добутку 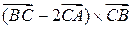 .
.
Варіант 24
1) При яких значеннях  і
і 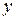 вектори
вектори  і
і 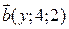 колінеарні.
колінеарні.
2) Визначити, при якому значенні t вектори 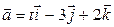 і
і 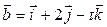 взаємно перпендикулярні.
взаємно перпендикулярні.
3) Обчислити площу трикутника з вершинами А(4; 2; 3), В(5; 1; 2),
С(6; 5; 8).
Варіант 25
1) Знайти довжину вектора  , якщо
, якщо  і
і 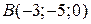 .
.
2) Задані вершини трикутника А(0; -1; 4), В(-3; -1; 0), С(4; -1; 1). Визначити його внутрішній кут при вершині В.
3) Вектори 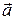 і
і  утворюють кут 1200,
утворюють кут 1200,  . Обчислити
. Обчислити 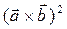 .
.
Варіант 26
1) При яких значеннях  вектори
вектори 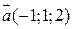 і
і 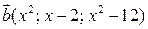 колінеарні.
колінеарні.
2) Вектор 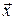 , перпендикулярний до векторів
, перпендикулярний до векторів 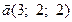 і
і 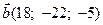 , утворює з віссю ОУ тупий кут і має довжину
, утворює з віссю ОУ тупий кут і має довжину 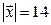 . Знайти його координати.
. Знайти його координати.
3) Обчислити мішаний добуток векторів 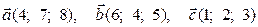 .
.
Варіант 27
1) Дано точки А(-1; 3; -3), В(4; 3; 6), С(2; 0; 3), D(4; 3; -3). Знайти проекцію вектора 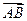 на вектор
на вектор  .
.
2) Дано три вектори  і
і 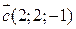 . Обчислити проекцію вектора
. Обчислити проекцію вектора 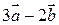 на вектор
на вектор  (
(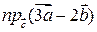 ).
).
3) Визначити, якою трійкою є трійка векторів, лівою чи правою 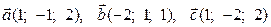 .
.
Варіант 28
1) При яких значеннях 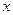 вектори
вектори  і
і 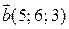 перпендикулярні.
перпендикулярні.
2) Знайти кут між ненульовими векторами 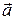 і
і  , якщо
, якщо 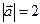 ,
, 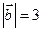 і справедлива рівність
і справедлива рівність 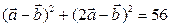 .
.
3) З’ясувати лінійну залежність векторів  .
.
Варіант 29
1) Визначити при яких значеннях 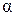 і
і 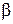 вектори
вектори  і
і 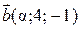 колінеарні.
колінеарні.
2) Вектори 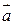 і
і 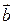 утворюють кут 300, причому
утворюють кут 300, причому 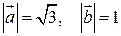 . Знайти кут між векторами
. Знайти кут між векторами 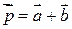 і
і 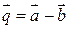 .
.
3) Знайти об’єм паралелепіпеда, побудованого на векторах  ,
,  .
.
Варіант 30
1)Заданий вектор 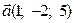 . Знайти координати вектора
. Знайти координати вектора  , який лежить у площині ХОУ і перпендикулярний до вектора
, який лежить у площині ХОУ і перпендикулярний до вектора 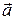 , якщо
, якщо 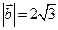 .
.
2) Знайти кут між діагоналями паралелограма, побудованого на векторах 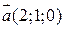 і
і 
3) Знайти об’єм паралелепіпеда, побудованого на векторах  ,
, 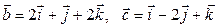 .
.
Не нашли, что искали? Воспользуйтесь поиском: