Расчет элементов металлических конструкций на изгиб.

Бетонные изгибаемые элементы рассчитывают из условия равнове­сия в предельном состоянии. Перед образованием трещин на растяну­той грани напряжения достигают величины R_bt а эпюра в растянутой зоне вследствие развития значительных пластических деформаций силь­но искривляется, что позволяет без большой погрешности заменить ее прямоугольной. Нормальные напряжения на сжатой грани существенно меньше предельных, поэтому эпюра напряжений в сжатой зоне может быть принята треугольной. Ее наклон принимают таким, чтобы при продолжении в растянутой зоне она отсекала на крайнем волокне отре­зок, равный 2 R_bt (рис. 4.1). Это условие равносильно принятию модуля

деформации крайнего растянутого волокна бетона равным половине модуля упругости при сжатии (Е' _bt = 0, 5Е_Ь).

Таким образом, за расчетную эпюру внутренних напряжений в бе­тонном сечении вместо фактической криволинейной принята треуголь­ная в сжатой зоне и прямоугольная в растянутой. Принимается справед­ливой также гипотеза плоских сечений.

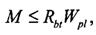Прочность для элементов произвольной формы сечения проверяют из условия

(4.2)

где W_pl — момент сопротивления для растянутой грани сечения, опреде­ляемый с учетом неупругих свойств бетона.

Для определения W_pl следует сначала найти положение нейтраль­ной оси, соответствующее принятой эпюре напряжений. Для этого со­ставляют уравнение проекций всех сил на продольную ось элемента, из которого получают статический момент сжатой

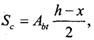площади сечения отно­сительно нейтральной оси

где А _bt — площадь растянутой зоны сечения.

В общем случае положение нейтральной оси, т.е. величину х, опре­деляют последовательным приближением. Однако для большинства встречающихся на практике видов сечений, а именно, когда нейтраль­ная ось заведомо пересекает участок сечения с постоянной шириной (пря­моугольное, тавровое, коробчатое и др.), выражение (4.2) легко преоб­разуют в уравнение с одним неизвестным, из которого можно непосред­ственно определить х.

Выражение упругопластического момента сопротивления сечения получим из уравнения моментов всех сил относительно нейтральной оси, из которого

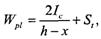
гдеlc — момент инерции сжатой зоны сечения относительно нулевой линии; S, — статический момент растянутой части сечения относитель­но той же оси.

Величину W_pl допускается определять также по формуле

W_pl=γW_el, (4.4)

т.е. умножениенм величины упругого момента сопротивления крайнего растянутого волокна сечения относительно оси, проходящий через центр тяжести сечения W_el, на коэффициент у, значения которого для сечения различной формы приводятся в пособиях по проектированию конструк­ций [10]*. Например, для прямоугольного и таврового сечения с полкой в сжатой зоне у = 1,75. Это свидетельствует о том, что учет неупругих деформаций в растянутой зоне существенно увеличивает расчетную проч­ность бетонных элементов, что хорошо согласуется с данными опытов. Элементы прямоугольной формы сечения допускается рассчитывать по формуле

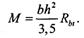
Не нашли, что искали? Воспользуйтесь поиском: