Система скважина-трещина-пласт

Рассмотрим вертикальную трещину, охватывающую всю толщину продуктивного пласта мощностью h, как показано на рис. 3-1.

РИС. 3-1. Обозначения для эффективности трещины.

Отметим, что в действительности форма областей дренирования ни прямоугольная, ни круглая, однако для большинства форм областей дренирования эти геометрические элементы являются разумными приближениями. Использование 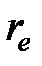или является всего лишь вопросом удобства. Соотношение между площадью дренирования , радиусом области дренирования r_e и длиной стороны площади дренирования x_e задается выражением

(3-10)

Известно, что для вертикальной скважины, пересекающей вертикальную трещину, которая полностью вскрывает прямоугольный дренируемый объем от подошвы до кровли, эффективность зависит от коэффициента вскрытия в направлении ,

, (3-11)

а также от безразмерной проводимости трещины,

, (3-12)

где — полудлина трещины, — длина стороны квадратной площади дренирования, — проницаемость пласта, — проницаемость проппантной набивки, а — средняя (расклиненная) ширина трещины.

Число проппанта

Ключ к формулированию содержательной технической оптимизационной задачи состоит в осознании того, что величина вскрытия трещины и безразмерная проводимость трещины (через ее ширину) соревнуются за один и тот же ресурс: расклиненный объем. Поскольку свойства пласта и проппанта, а также объем проппанта — величины фиксированные, то приходится выбирать оптимальный компромисс между шириной и длиной. Имеющийся расклиненный объем накладывает ограничение на эти две безразмерные величины. Чтобы легко оперировать с этим ограничением, мы вводим безразмерное число проппанта:

(3-13)

Согласно приведенному выше определению, число проппанта есть просто комбинация двух других безразмерных параметров: коэффициента вскрытия и безразмерной проводимости трещины. Подставляя определение коэффициента вскрытия и безразмерной проводимости в уравнение 3-13, получаем

(3-14)

где — число проппанта, безразмерная величина; — эффективная проницаемость упаковки проппанта, мД; — проницаемость пласта, мД; — расклиненный объем в продуктивном пласте (два крыла, включая пустое объем пустот между зернами проппанта), фут³; и — дренируемый объем (т.е., площадь дренирования, помноженная на толщину продуктивного пласта), фут³. (Конечно, могут быть использованы любые другие когерентные единицы, поскольку в число проппанта входят только отношение проницаемостей и отношение объемов).

Уравнение 3-14 ясно выявляет, что означает число проппанта: это есть взвешенное отношение расклиненного объема трещины (два крыла) к объему резервуара, где весовой коэффициент равен удвоенному отношению проницаемости проппанта к проницаемости пласта. Отметьте, что в расклиненном объеме учитывается только тот проппант, который достиг продуктивного пласта. Если, например, высота трещины в три раза больше мощности продуктивного пласта, то можно оценить как насыпной объем (упакованного) нагнетенного проппанта, поделенный на три. Другими словами, упакованный объем нагнетенного проппанта, помноженный на объемную эффективность проппанта, дает объем , используемый в расчете числа проппанта.

Безразмерное число проппанта, , и есть самый наиважнейший параметр в унифицированном дизайне гидроразрыва.

На рис. 3-2 показан традиционный вид зависимости как функции безразмерной проводимости трещины, , где используется как параметр. Аналогичные графики, показывающие увеличение продуктивности, являются обычными в публикуемой литературе.

Однако, рис. 3-2 не очень-то помогает в решении задачи оптимизации при фиксированном объеме проппанта. Для этой цели мы приводим рис. 3-3 и 3-4, где показаны те же результаты, но в качестве параметра используется число проппанта, . Отдельные кривые соответствуют для фиксированного значения числа проппанта.

Как видно из рис. 3-3 и 3-4, для заданного значения максимальный индекс продуктивности достигается при строго определенной безразмерной проводимости трещины. Поскольку заданное число проппанта представляет фиксированный объем проппанта, достигающего продуктивного горизонта, то наилучший компромисс между длиной и шириной достигается при безразмерной проводимости трещины, расположенной в районе пика отдельных кривых.

РИС. 3-2. Безразмерный индекс продуктивности как функция безразмерной проводимости трещины, параметр — I_x (представление Макгвайра-Сикоры)

Один из главных результатов, который виден из этих рисунков, — это то, что при числах проппанта меньше 0.1 такой оптимальный компромисс всегда имеет место при C_fD = 1.6. При возрастании расклиненного объема оптимальный компромисс имеет место при более высоких безразмерных проводимостях трещины, просто потому, что безразмерный коэффициент вскрытия пласта не может быть больше единицы (т.е., когда трещина доходит до границы продуктивного пласта, дополнительный проппант тратится только на увеличение ширины трещины). Этот эффект показан на рис. 3-4, из которого видно, что абсолютный максимум, которого может достигнуть безразмерный индекс продуктивности, равен 1.909. Абсолютное максимальное значение ИП, равное , есть индекс продуктивности, соответствующий идеальному линейному потоку в квадратном пласте.

В пластах средней и высокой проницаемости (выше 50 мД) практически невозможно достигнуть числа проппанта больше 0.1. Для гидроразрыва типа фрак-пак, типичные числа проппанта лежат в диапазоне от 0.0001 до 0.01. Таким образом, для пластов от средней до высокой проницаемости оптимальная безразмерная проводимость трещины всегда составляет .

В «плотных газовых» пластах можно достигнуть высоких безразмерных чисел проппанта, по крайней мере, в принципе. Числа проппанта, рассчитанные для ограниченной области дренирования — не входя в рассуждения относительно доли проппанта, фактически находящегося в продуктивном пласте — может достигать столь высоких величин, как от 1 до 10. Однако на практике может быть трудно добиться чисел проппанта больше 1. При крупнообъемных гидроразрывах проппант может мигрировать вверх, создавая излишнюю и незапланированную высоту трещины, или же он может проникнуть по латерали за пределы планируемой области дренирования.

РИС. 3-3. Безразмерный индекс продуктивности как функция безразмерной проводимости трещины, параметр — число проппанта (для N_prop < 0.1).

РИС. 3-4. Безразмерный индекс продуктивности как функция безразмерной проводимости трещины, параметр — число проппанта (для N_prop > 0.1).

Для одиночной скважины в области большего размера ситуация более сложная. В этом случае (гипотетическая) большая длина трещины стремится увеличить дренируемый объем пласта, и числа проппанта уменьшаются. В конечном счете, большая трещина выгодна, но достижимые числа проппанта остаются ограниченными.

На деле же было бы чрезвычайно сложно даже попытаться достигнуть чисел проппанта больше единицы. На самом деле, для больших чисел проппанта оптимальная 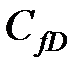определяет оптимальный коэффициент вскрытия близкий к единице. Этот случай легко видеть на рис. 3-5, где коэффициент вскрытия показан по оси х. Чтобы разместить проппант «от стенки до стенки», удержав его в то же время в пределах дренируемого объема, потребовалась бы столь высокая точность операции по гидроразрыву, которой невозможно добиться на практике.

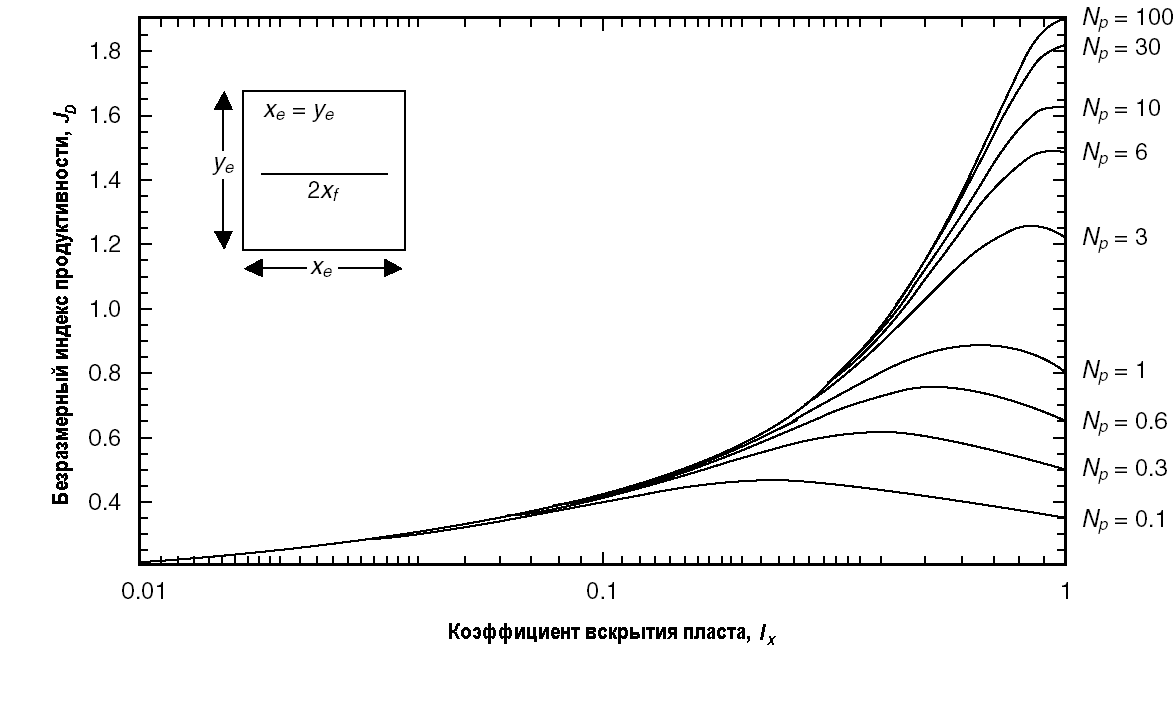
РИС. 3-5. Безразмерный индекс продуктивности как функция коэффициента вскрытия пласта, параметр — число проппанта (для N_prop > 0.1).

Максимально возможный безразмерный индекс продуктивности для составляет примерно . Безразмерный индекс продуктивности неповрежденной вертикальной скважины равен от 0.12 до 0.14, в зависимости от расстояния между скважинами и принятого радиуса скважины. Следовательно, имеется реалистический максимум «кратного увеличения» индекса продуктивности для псевдостационарного режима (относительно случая нулевого скина), приблизительно равный 7, т.е., 0.9 поделенное на 0.13. Более высокие кратности маловероятны. Конечно, более высокие кратности могут быть достигнуты относительно изначально поврежденной скважины, где скин-фактор до обработки имеет большую положительную величину.

Другое распространенное недопонимание связано с периодом неустановившегося течения. При неустановившемся притоке индекс продуктивности (и, следовательно, дебит) больше, чем в псевдостационарном случае. Имея в голове такую качественную картину, становится легко отбросить процедуру оптимизации для псевдостациораного режима и «нацеливаться» на очень высокие безразмерные проводимости трещины и/или ожидать намного более высокой кратности возрастания продуктивности. На самом же деле, существование неустановившегося режима потока не меняет предшествующих выводов относительно оптимальных размеров ГРП. Наши расчеты показывают, что нет причин отходить от оптимального компромисса, выведенного для псевдостационарного случая, даже если скважина будет значительное время (скажем, месяцы или даже годы) работать в переходном режиме. Попросту говоря, что хорошо для псевдостационарного притока, хорошо и для максимизации неустановившегося притока.

В определении числа проппанта — это эффективная (или эквивалентная, как ее иногда называют) проницаемость проппантной набивки. Это наиболее важный параметр в дизайне. Существующие ныне компьютерные модели гидроразрыва обычно используют для проппантной набивки номинальное значение (даваемое производителем проппанта) и позволяют уменьшить его на некоторый множитель, который предлагается выбирать пользователю. В расчетах числа проппанта необходимо использовать уже уменьшенное значение.

Имеется множество причин, почему фактическая (или эквивалентная) проницаемость проппантной набивки будет меньше номинального значения. Основные причины следующие:

n Большие напряжения смыкания трещины дробят проппант, уменьшая средний размер зерен, однородность зерен и пористость.

n Остатки жидкости разрыва уменьшают проницаемость трещины.

n Высокие скорости потока флюида в проппантной набивке создают «эффекты отклонения от закона Дарси» (или «эффекты неньютоновского течения»), приводящие к дополнительным потерям давления. Это явление может быть значительным при добыче газа в присутствии жидкости (воды и/или конденсата). Этот неньютоновский эффект вызван периодическим ускорением / замедлением капель жидкости, которое эффективно уменьшает проницаемость проппантной набивки. Такая уменьшенная проницаемость может быть на порядок ниже номинального значения, представленного производителем.

При проектировании гидроразрыва необходимо уделять большое внимание эффективной проницаемости проппантной набивки и проницаемости пласта. Знание действующего контраста проницаемостей чрезвычайно важно, и его никоим образом нельзя подменять качественными рассуждениями.

Не нашли, что искали? Воспользуйтесь поиском: