Линейная упругость и механика трещинообразования

Упругость подразумевает обратимые изменения. Зарождение и распространение трещины означает, что материал отреагировал существенно неупругим образом, и произошло необратимое изменение. Тем не менее, линейная упругость является полезным инструментом при изучении трещин, поскольку напряжения и деформации (за исключением, пожалуй, окрестностей поверхности трещины и особенно ее верхушки) могут быть достаточно адекватно описаны при помощи теории упругости.

Линейно упругий материал характеризуется упругими постоянными, которые можно определить в экспериментах по статическому или динамическому нагружению. Для изотропного материала, когда свойства не зависят он направления, для описания его поведения достаточно двух постоянных.

На рис. 1-4 схематически представлен статический эксперимент с одноосным нагружением. Два параметра, определяемые из такого эксперимента, — это модуль Юнга ()и коэффициент Пуассона (). Они рассчитываются из вертикального напряжения (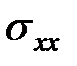), вертикальной деформации (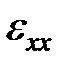), и горизонтальной деформации (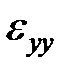), как показано на рисунке.

В табл. 4-1 показана взаимосвязь тех постоянных, которые чаще всего используются в гидроразрыве. Модуль плоской деформации (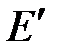) — это единственная константа упругости, действительно нужная в наших уравнениях.

В линейной теории упругости для уменьшения размерности задачи часто используется концепция плоской деформации. Принимается, что тело является бесконечным по крайней мере в одном направлении, а внешние силы (если таковые имеются) приложены параллельно этому направлению (т.е., «бесконечно повторяются» в каждом поперечном сечении). В таком случае интуитивно очевидно, что деформация также бесконечно повторяет сама себя.

Плоская деформация является разумной аппроксимацией в упрощенном описании гидроразрыва пласта. Главный вопрос состоит в том, как выбрать эту плоскость. Возникают две возможности, и, в свою очередь, это дало начало двум различным подходам к моделированию трещины. Кристианович и Желтов [Khristianovitch and Zheltov, 1955], а также Геертсма и де Клерк [Geertsma and de Klerk, 1969] приняли состояние деформации в горизонтальной плоскости, тогда как Перкинс и Керн [Perkins and Kern, 1961] и Нордгрен [Nordgren, 1972] приняли плоскую деформацию в вертикальной плоскости (нормальной к направлению распространения трещины).

В литературе по гидроразрыву для допущения о плоской деформации в горизонтальной плоскости зачастую применяется термин «геометрия KGD», а для постулированной плоской деформации в вертикальное плоскости применяется термин «геометрия PKN».

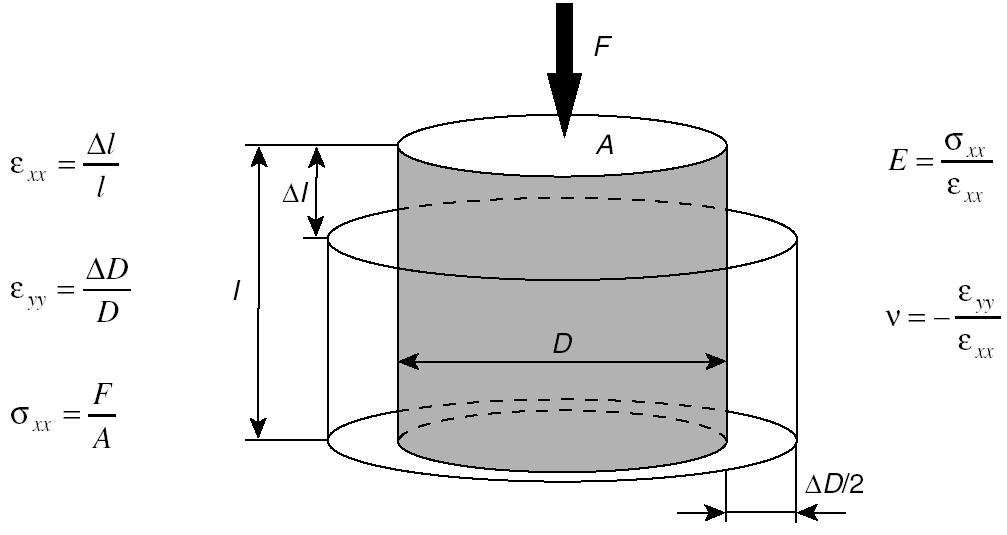
Рис. 4-1. Эксперимент по одноосному нагружению.

Таблица 4-1. Взаимосвязь различных свойств линейно-упругого материала
Искомое/известное	E,n	G,n	E, G
Модуль сдвига, G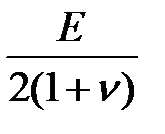
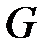
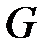
Модуль Юнга, E
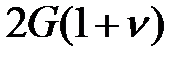
Коэффициент Пуассона, n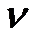
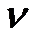
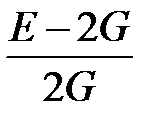
Модуль плоской деформации,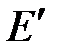

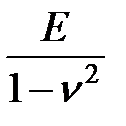
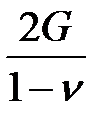
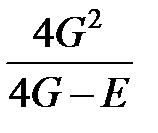
Имеются точные математические решения для задачи о трещине с поддерживаемом внутри нее давлением в состоянии плоской деформации. В частности, известно, что линейная трещина с давлением внутри имеет эллиптическое распределение ширины [Sneddon, 1973]:

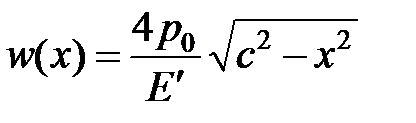(4-1)

где — расстояние от центра трещины, 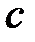— полудлина (расстояние от фронта до центра), а 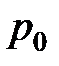— постоянное давление, действующее на стороны трещины изнутри. Из уравнения 4-1 максимальная ширина в центре равна

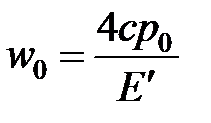, (4-2)

что указывает на то, что поддерживается линейное отношение между вызванным раскрытием трещины и приложенным давлением. Когда концепция раздуваемой трещины применяется к реальной ситуации, то 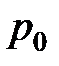заменяется на эффективное давление, , определяемое как разность между внутренним давлением и наименьшим главным напряжением, действующим снаружи и пытающимся сомкнуть эту трещину [Hubbert and Willis, 1957; Haimson and Fairhurst, 1967].

Механика трещины возникла из наблюдения, что любая неоднородность, существующая в твердом теле, ухудшает его способность выдерживать нагрузки. Отверстие (возможно, небольшое) может привести к появлению высоких локальных напряжений по сравнению с напряжениями, которые имели бы место без этого отверстия. Высокие напряжения, даже если они проявляются на малой площади, могут привести к разрушению материала. Часто бывает удобно рассматривать неоднородности в материале как концентраторы напряжений, которые локально увеличивают напряжения, имеющие место без них.

Необходимо различать два основных случая. Если форма неоднородности гладкая (например, круглая скважина в пласте), то максимальное напряжение вокруг этой неоднородности выше исходного напряжения на некоторый множитель, зависящий от геометрии. Например, коэффициент концентрации напряжений для круглой скважины равен трем.

Иная ситуация наблюдается в случае острых краев, таких как вершина трещины. Тогда максимальное напряжение на этой вершине становится бесконечным. В механике трещины нам приходится иметь дело с особыми точками функций. Два разных нагружения (распределения давлений) у линейной трещины приводят к двум разным распределениям напряжений. Оба этих случая могут дать бесконечные напряжения на вершине, но «уровень бесконечности» при этом различный. Нам необходимо охарактеризовать это различие при помощи некоторой величины. К счастью, все распределения напряжений вблизи вершины любой трещины аналогичны в том смысле, что они убывают по закону 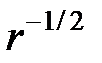, где 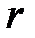есть расстояние от вершины. Величина, используемая для характеристики «уровня бесконечности» — это коэффициент интенсивности напряжений 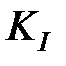, определяемый как множитель функции 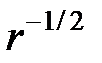. Для идеализации в виде линейной трещины с давлением внутри, имеющей полудлину 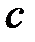, и постоянное давление 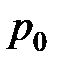, коэффициент интенсивности напряжений задается выражением

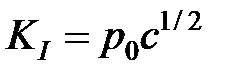(4-3)

Иными словами, коэффициент интенсивности напряжений на вершине трещины пропорционален постоянному давлению, раскрывающему эту трещину, и квадратному корню ее полудлины (характеристического размера).

Согласно ключевому постулату линейно-упругой механики трещины, для любого данного материала имеется некоторое критическое значение коэффициента интенсивности напряжений, 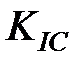, называемое вязкостью разрушения (или трещиностойкостью). Если коэффициент интенсивности напряжений на вершине трещины выше этого критического значения, трещина будет распространяться, в противном случае — нет. Вязкость разрушения является полезной величиной для расчетов безопасности, когда единственная забота инженера состоит в том, чтобы избежать образования трещин. Однако, в стимуляции скважин, где главная цель инженера — создать и распространить трещину, эта концепция обнаруживает некоторую противоречивость, поскольку она предсказывает, что для распространения трещины требуется всё меньше и меньше усилий по мере увеличения ее размеров. По большому же счету, обычно верно обратное.

Не нашли, что искали? Воспользуйтесь поиском: