Формальный материальный баланс: коэффициент распределения времени раскрытия трещины

Рассмотрим процесс гидроразрыва, схематически изображенный на рис. 4-3. Объем , нагнетенный в одно крыло за время , состоит из двух частей: объема одного крыла трещины в конце нагнетания (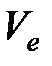) и потерянного объема (объема утечки). Нижний индекс 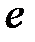обозначает, что данное количество измерено в конце закачки или относится к этому моменту времени. Отметьте, что все переменные определены относительно одного крыла. Площадь обозначает поверхность одной стороны одного крыла трещины. Эффективность (коэффициент использования) жидкости определяется как доля жидкости, остающаяся в трещине: 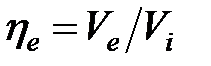. Средняя ширина, 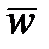, определяется выражением .

Операция гидроразрыва пласта может длиться от десятков минут до нескольких часов. Точки на поверхности трещины, расположенные вблизи скважины, были «раскрыты» в самом начале нагнетания, тогда как точки вблизи вершины трещины моложе. Применение уравнения 4-5 заставляет отслеживать время раскрытия для различных элементов поверхности трещины.

Если рассматривается только суммарный материальный баланс, то вполне естественно переписать нагнетенный объем как сумму объема трещины, объема утечки и объема мгновенной утечки, используя следующее формальное представление:

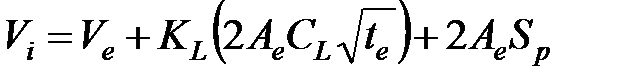(4-6)

где переменная есть коэффициент распределения времени раскрытия. Он отражает историю эволюции поверхности трещины, или скорее распределение времени ее раскрытия, отсюда и его название. В частности, если вся поверхность трещины раскрылась в начале нагнетания, то достигает своего абсолютного максимума, 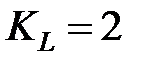. Эффективность жидкости есть отношение созданного объема трещины к нагнетенному объему. Поделив оба объема на конечную площадь трещины, мы можем рассматривать эффективность трещины как отношение созданной ширины к ширине, которая могла бы быть создана, где ширина, которая могла бы быть создана, определяется как сумма созданной и потерянной ширины.

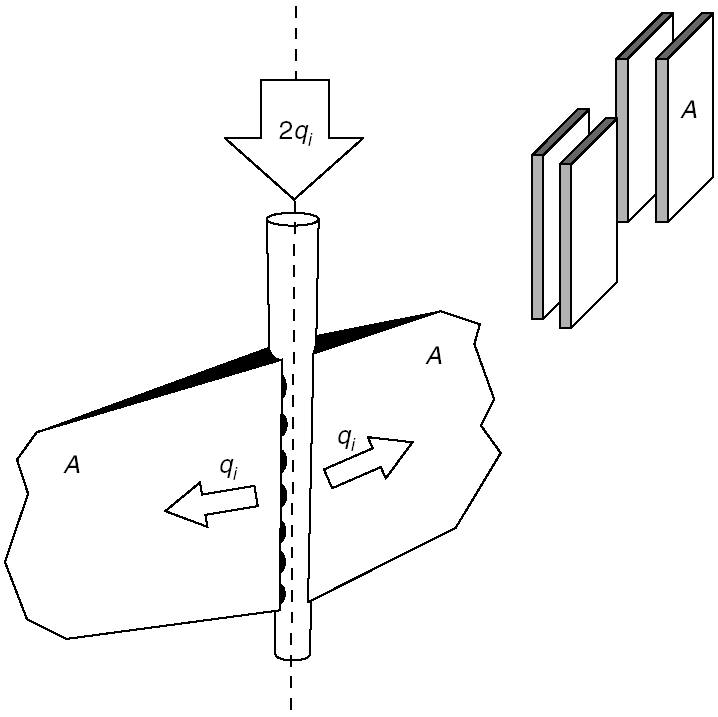
РИС. 4-3. Условные обозначения для материального баланса.

Поэтому другая форма уравнения 4-6 следующая:

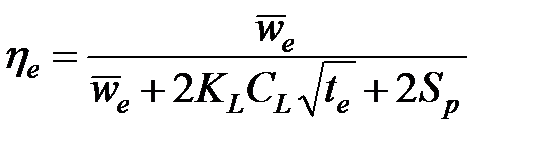(4-7)

Она показывает, что член 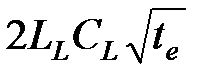можно рассматривать как «ширину утечки», а член 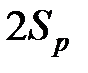— как «ширину мгновенной утечки». Уравнение 4-7 можно преобразовать, чтобы получить коэффициент распределения времени раскрытия, выраженный через эффективность жидкости и среднюю ширину в конце нагнетания:

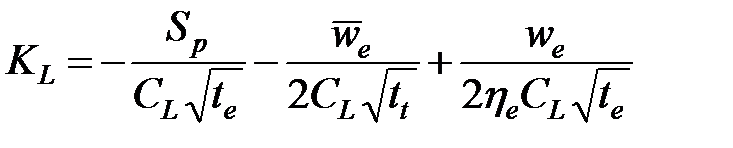(4-8)

Отметьте, что эти выражения не зависят от фактической формы поверхности трещины или от истории ее эволюции.

Аппроксимация постоянной ширины (уравнение Картера II)

Чтобы получить аналитическое решение для постоянного темпа нагнетания, Картер рассмотрел гипотетический случай, при котором ширина трещины остается постоянной в течение всего времени распространения трещины (ширина «скачком» достигает своего конечного значения в первое мгновение нагнетания). Тогда можно получить аналитическое выражение для эффективнсоти жидкости, выраженное через два параметра утечки и ширину:

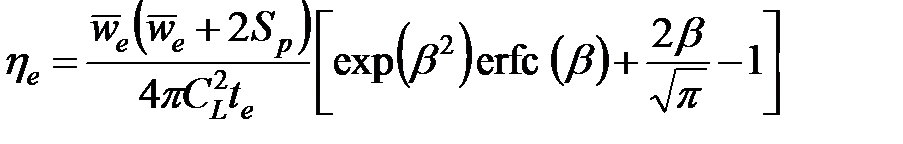(4-9)

где .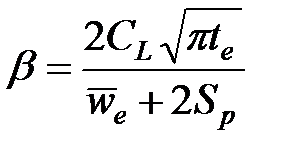

Не нашли, что искали? Воспользуйтесь поиском: