Механика жидкостей разрыва

Текучие материалы (флюиды) деформируются непрерывно (иными словами, текут) без разрушения под воздействием постоянного напряжения. Твердые тела обычно принимают состояние статического равновесия под действием таких же напряжений. Сшитые (полимерные) жидкости разрыва обычно ведут себя как вязкоупругие жидкости. Их функции напряжение-деформация находятся между такими функциями для чистых жидкостей и твердых тел.

С нашей точки зрения, наиболее важным свойством жидкостей является их сопротивление течению. Локальная интенсивность течения характеризуется скоростью сдвига, 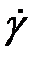, измеряемой в 1/с. Ее можно рассматривать как темп изменения скорости с расстоянием между скользящими слоями. Напряжение, возникающее между слоями, есть напряжение сдвига, . Его размерность — сила на единицу площади (в системе СИ — Па). Материальная функция, выражающая связь между напряжением сдвига и скоростью сдвига — реологическая кривая. Эта информация необходима для расчета падения давления (фактически, рассеяния энергии) для заданной ситуации течения, такое как течение в трубе или течение между параллельными пластинами.

Кажущаяся вязкость определяется как отношение напряжения к скорости сдвига. Как правило, кажущаяся вязкость изменяется со скоростью сдвига, за исключением случая ньютоновской жидкости — весьма специфической жидкости, вязкость которой постоянна. Реологическая кривая и кривая кажущейся вязкости содержат одну и ту же информацию и используются взаимозаменяемо. На рис. 4-2 показаны типичные реологические кривые, а в табл. 4-2 перечислены некоторые обычно используемые реологические уравнения состояния.

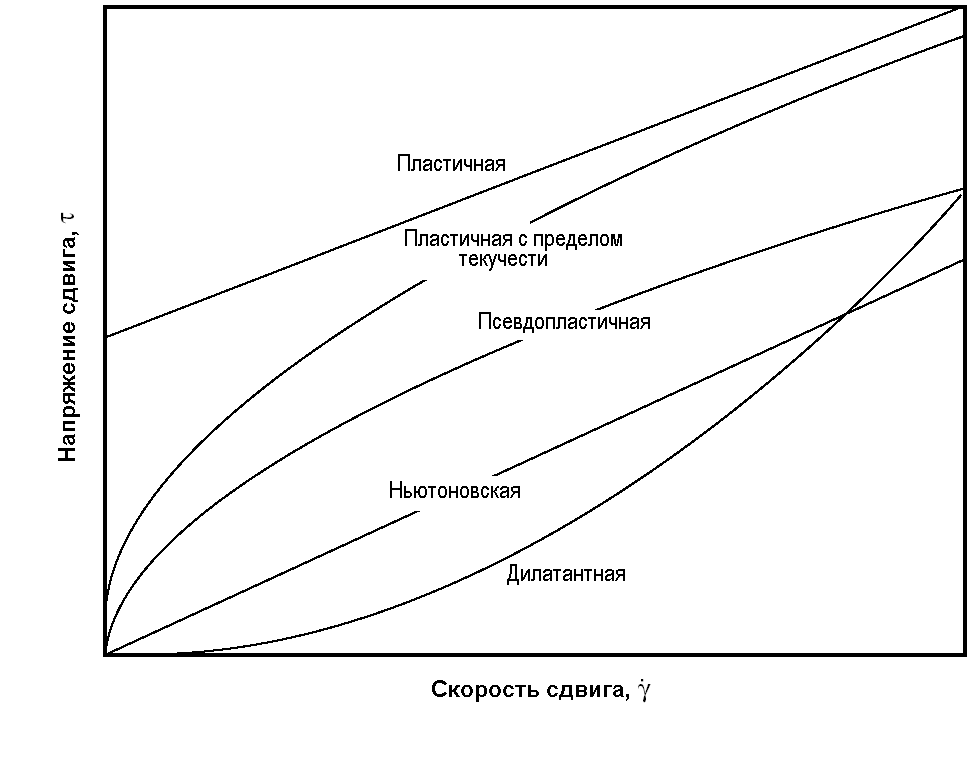
РИС. 4-2. Типичные реологические кривые.

Таблица 4-2. Обычно используемые реологические уравнения состояния
	Ньютоновская жидкость
	Степенной закон
	Бингемовская пластичная жидкость
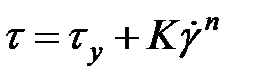
	Степенной закон с пределом текучести

Параметры модели меняются с химическим составом, температурой и, в меньшей степени, многими другими факторами, включая историю сдвига. В случае пен, важную роль играет отношение объемов газовой и жидкой фаз [Reidenbach, 1985; Winkler, 1995].

Большинство гелей гидроразрыва проявляют значительное разжижение при сдвиге (т.е., уменьшение вязкости с увеличением скорости сдвига). Уравнение состояния, описывающее этот главный аспект их режима течения, — модель степенного закона. Показатель текучести, n, обычно изменяется от 0.3 до 0.6.

Все флюиды проявляют некоторую конечную граничную вязкость при высоких скоростях сдвига. Для определенных жидкостей нарастание кажущейся вязкости до очень высоких значений при низких скоростях сдвига может быть аппроксимировано включением предела текучести. Многие жидкости демонстрируют при низких скоростях сдвига текучесть, выглядящую как ньютоновская.

Многие из текущих реологических исследований сфокусированы на построении более реалистичных моделей, эффективно включающих каждую из вышеупомянутых характеристик, таких как нелинейные, времязависимые вязкоупругие эффекты сшитых (кросслинованных) полимерных гелей.

Реологическая модель используется для предсказания потерь (градиента) давления, связанных со средней скоростью течения в заданной физической геометрии. Уравнения движения решены для стандартных реологических моделей в наиболее очевидных геометриях (напр., течение в круглых трубах, кольцевых пространствах, а также в тонкой щели между параллельными пластинами). Такие решения зачастую представлены как связь между средней линейной скоростью (расход жидкости на единицу площади) и радением давления. В вычислениях удобно использовать эквивалентную ньютоновскую вязкость (), то есть, вязкость, которая использовалась бы в уравнении для ньютоновской жидкости, чтобы получить то же самое падение давления при тех же самых условиях течения. Тогда как кажущаяся вязкость (при данной локальной скорости сдвига) есть свойство жидкости, эквивалентная вязкость зависит также от геометрии потока и несет в себе ту же информацию, что и решение для падения давления. Для более сложных реологических моделей, решений в аналитическом виде нет (ни для падения давления, ни для эквивалентной ньютоновской вязкости), и вычисления производятся с помощью различных численных методов.

Особый интерес для гидроразрыва представляет ламинарное течение для двух предельных геометрий. Щелевое течение имеет место в канале прямоугольного сечения, когда отношение длины большей стороны к длине меньшей чрезвычайно велико. Предельное эллипсоидальное течение имеет место в эллиптическом поперечном сечении с чрезвычайно большим относительным удлинением. Первое соответствует геометрии KGD, а второе — геометрии PKN.

В таблице 4-1 приведены решения, обычно используемые в расчетах по гидроразрыву. Первым приведено самое знакомое уравнение, действительное для ньютоновской жидкости. Затем дается эквивалентная вязкость для жидкости, подчиняющейся степенному закону. Эквивалентная вязкость может быть использована в ньютоновской форме уравнения падения давления. Обратите внимание, что эквивалентная вязкость зависит от средней скорости () и от геометрии канала (в случае потока в щели от ширины, 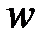; в случае эллиптического поперечного сечения — от максимальной ширины, ). Интересно отметить, что уравнение для ламинарного течения жидкости, подчиняющейся степенному закону, в предельной эллипсоидальной геометрии не выведено. Представленное здесь решение может быть получено методом аналогии (подробности см. в [Valkó and Economides, 1995]).

ТАБЛИЦА 4-3. Падение давления и эквивалентная ньютоновская вязкость
Реологическая модель	Ньютоновская	Степенной закон
Щелевое течение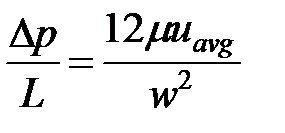
Эллипсоидальное течение

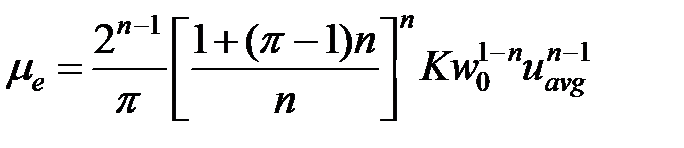
Потери давления на трение, связанные с нагнетанием жидкостей разрыва через поверхностные трубопроводы и систему труб скважины не могут быть рассчитаны непосредственно с использованием классических корреляционных зависимостей для турбулентного течения. Для учета явлений уменьшения сопротивления, вызываемых длинными полимерными цепочками, приходится применять специальные зависимости. Реологическое поведение также играет важную роль в способности жидкости переносить проппант [Roodhart, 1985; Acharya, 1986].

Не нашли, что искали? Воспользуйтесь поиском: