Аппроксимация роста трещины степенным законом

Основное допущение, сформулированное Нольте [Nolte, 1979, 1986] приводит к замечательно простой форме материального баланса. Он принял, что поверхность трещины развивается по степенному закону,

(4-10)

где и , а показатель степени 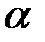остается постоянным в течение всего времени нагнетания. Нольте выяснил, что в этом случае коэффициент распределения времени является функцией только показателя степени a. Он представил коэффициент распределения времени раскрытия и его зависимость от показателя степени в выражении для роста поверхности трещины, использовав обозначение , и представил для избранных значений 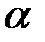. Для коэффициента времени раскрытия трещины для любых 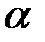может быть использовано простое выражение, впервые полученное Хагелем и Мейером [Hagel and Meyer, 1989]:

(4-11)

где — гамма-функция Эйлера.

При расчетах может быть, проще использовать следующую аппроксимацию функции :

(4-12)

Нольте принял, что показатель степени остается между 0.5 и 1. При этом допущении коэффициент лежит между 4/3 (1.33) и p/2 (1.57), что указывает на то, что для двух кардинально различающихся историй роста поверхности коэффициент распределения времени раскрытия изменяется меньше чем на 20 процентов. Как правило, простая аппроксимация должна обеспечить достаточную точность для целей проектирования.

Различные исследователи изучали связь показателя степени 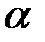с геометрией трещины, коэффициентом использования жидкости в конце нагнетания, а также с реологическими свойствами жидкости. Ни одна из этих связей не может считаться теоретически доказанной, но они представляют собой разумные инженерные приближения, особенно по той причине, что влияние этого показателя степени на конечный результат ограниченное. Мы рекомендуем использовать 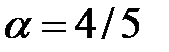для геометрии PKN, 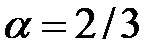для геометрии KGD, и для радиальной модели. Эти показатели степени могут быть выведены из уравнений для нелевой утечки, как показано ниже в таблице 4-4.

В числовом отношении первоначальная аппроксимация Картера для постоянной ширины и допущение Нольте о степенном законе роста дают очень близкие результаты, если их использовать для целей проектирования. Однако, подход с использованием функции имеет технические преимущества для анализа калибровочных обработок.

Не нашли, что искали? Воспользуйтесь поиском: