
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Четырехмерный потенциал поля
Рассмотрим частицу, движущаяся в электромагнитном поле. Функция действия для этой частицы складывается из двух частей: из действия (2.1) свободной частицы и из члена, описывающего взаимодействие частицы с полем. Последний должен содержать величины, характеризующие частицу, и величины, характеризующие поле.
Опыт показывает, что свойства частицы в отношении ее взаимодействия с электромагнитным полем определяют всего одним параметром – так называемом зарядом частицы  , причем
, причем  либо >0, либо <0, либо =0. Свойства поля характеризуется 4-вектором A:, так называемым 4-потенциалом, компоненты которого являются функциями координат и времени. Это также подтверждаются опытом. Эти величины входят в действие в виде члена
либо >0, либо <0, либо =0. Свойства поля характеризуется 4-вектором A:, так называемым 4-потенциалом, компоненты которого являются функциями координат и времени. Это также подтверждаются опытом. Эти величины входят в действие в виде члена

где функции  берутся в точках мировой линии частицы. Множитель
берутся в точках мировой линии частицы. Множитель 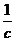 введен здесь для удобства.
введен здесь для удобства.
Итак,
 (3.1)
(3.1)
Три пространственные компоненты 4-вектора  образуют трехмерный потенциал
образуют трехмерный потенциал  , называемый векторным потенциалом поля. Временная компонента 4-вектора
, называемый векторным потенциалом поля. Временная компонента 4-вектора  мнима, т.е. имеет вид
мнима, т.е. имеет вид  . Действительная величина
. Действительная величина 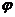 называется скалярным потенциалом поля. Таким образом
называется скалярным потенциалом поля. Таким образом
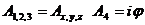 (3.2)
(3.2)
(3.1) можно переписать в виде

или переходя к интегрированию по времени
 (3.3)
(3.3)
где 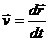 скорость частицы
скорость частицы
Функция Лагранжа  в соответствии с (3.3)
в соответствии с (3.3)
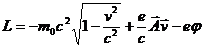 (3.4)
(3.4)
Это выражение отличается от функции Лагранжа для свободной частицы членами  , которые описывают взаимодействие заряда с полем.
, которые описывают взаимодействие заряда с полем.
Производная 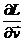 называется обобщенным импульсом частицы. Обозначим его непосредственно
называется обобщенным импульсом частицы. Обозначим его непосредственно 
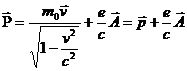 (3.5)
(3.5)
Здесь 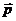 - обычный импульс частицы, который мы и будем называть простым импульсом.
- обычный импульс частицы, который мы и будем называть простым импульсом.
Функция Гамильтона частицы

Имеет в нашем случае
 (3.6)
(3.6)
Однако это не окончательно выражение, т.к. H должна быть выражена через импульс  частицы а не через скорость.
частицы а не через скорость.
Из (3.5) и (3.6) следует, что соотношения между  и
и  такое же, как и между
такое же, как и между 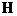 и
и  при отсутствии поля, т.е.
при отсутствии поля, т.е.
 (3.7)
(3.7)
или иначе
 (3.8)
(3.8)
Для малых скоростей, т.е. в классической механике, функция Лагранжа (3.4) переходит в
 (3.9)
(3.9)
В этом приближении


и мы находим следующие приближение для функции Гамильтона
 (3.10)
(3.10)
Уравнение Гамильтона Якоби, очевидно, имеет вид
 (3.11)
(3.11)
Оно получится из (3.7) заменой 
Не нашли, что искали? Воспользуйтесь поиском: