
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Четырехмерные векторы и тензоры.
Если пользоваться в качестве координат события величинами  , то мы можем рассматривать
, то мы можем рассматривать  как компоненты вектора в 4-х пространстве. Сумма квадратов компонент этого вектора, т.е. квадрат «длины»
как компоненты вектора в 4-х пространстве. Сумма квадратов компонент этого вектора, т.е. квадрат «длины»  , не меняется при поворотах 4-х мерной системы координат, которыми, в частности, являются преобразования Лоренца.
, не меняется при поворотах 4-х мерной системы координат, которыми, в частности, являются преобразования Лоренца.
Вектор с компонентами  называют 4-х мерным радиусом – вектором. Его компоненты будем обозначать через
называют 4-х мерным радиусом – вектором. Его компоненты будем обозначать через 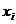 , где i = 1, 2, 3, 4, причем
, где i = 1, 2, 3, 4, причем

В соответствии с (1.15) при преобразовании от одной и.с.о. к другой, компоненты 4-х радиус-вектора преобразуются по формулам
 (1.25)
(1.25)
Четырех мерным вектором (4- вектором)  называется совокупность четырех величин
называется совокупность четырех величин  , которые при преобразовании 4-х мерной системы координат преобразовываются как компоненты
, которые при преобразовании 4-х мерной системы координат преобразовываются как компоненты 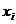 . При преобразовании Лоренца.
. При преобразовании Лоренца.
 (1.26)
(1.26)
Четырех мерные векторы обладают свойствами во многом аналогичными свойствам обычных векторов. Так, легко показать, что обычному скалярному произведению векторов сумма произведений компонент двух 4-х векторов  является скаляром. Мы будем обозначать ниже такое скалярное произведение, как
является скаляром. Мы будем обозначать ниже такое скалярное произведение, как  и вообще будем считать, что если один и тот же латинский индекс повторяется дважды, то подразумевается суммирование этого индекса. Компоненты 3-х мерных векторов мы будем обозначать греческими индексами; по дважды повторяющимися греческим индексам также будем подразумевать суммирование (например
и вообще будем считать, что если один и тот же латинский индекс повторяется дважды, то подразумевается суммирование этого индекса. Компоненты 3-х мерных векторов мы будем обозначать греческими индексами; по дважды повторяющимися греческим индексам также будем подразумевать суммирование (например 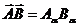 ) Первые три компоненты 4-х вектора будем называть пространственными, а четвертые – временной по аналогии с 4-радиусом – вектором. Временная компонента всех 4-х векторов, с которыми нам придется иметь дело,- мнимая.
) Первые три компоненты 4-х вектора будем называть пространственными, а четвертые – временной по аналогии с 4-радиусом – вектором. Временная компонента всех 4-х векторов, с которыми нам придется иметь дело,- мнимая.
Четырех мерным тензором (4-тензором) 2-го ранга называется совокупность шестнадцати величин  , которые при преобразовании координат
, которые при преобразовании координат
 (1.27)
(1.27)
преобразуются по формулам (т.е. компоненты тензора преобразуются как произведения координат)
 (1.28)
(1.28)
При преобразовании Лоренца
 (1.29)
(1.29)
Единичным 4-тензором  называется тензор с компонентами
называется тензор с компонентами

 (1.30)
(1.30)
Очевидно
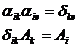 (1.31)
(1.31)
Следом тензора  , обозначаемыми как
, обозначаемыми как  называется скаляр
называется скаляр  , очевидно
, очевидно
 =4 (1.32)
=4 (1.32)
Тензор называется симметричным, если 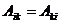 , и антисимметричными, если
, и антисимметричными, если  .
.
Аналогично 4 – тензору 2 ранга можно определить тензоры высших рангов.
Не нашли, что искали? Воспользуйтесь поиском: