Энергия и импульс частицы. Релятивистская масса.

По определению импульс частицы 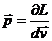. Учитывая (2.2), находим для частицы

(2.3)

При малых скоростях , т.е. имеем классическое выражение. При .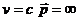

Производная от импульса по времени есть сила 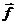, действующая на частицу. Пусть скорость частицы изменяется по направлению, т.е. сила направлена перпендикулярно скорости. Тогда

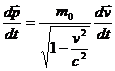(2.4)

Если же скорость изменяется только по величине, т.е. сила направлена по скорости, то

(2.5)

Энергией частицы называется, как известно, величина

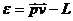
Подставляя (2.2) и (2.3) в это выражение, получим

(2.6)

Эта очень важная формула показывает, что в релятивистской механики энергия свободной частицы не обращается в нуль при 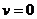, а остается конечной величиной, равной

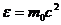(2.7)

Ее называют энергией покоя частицы

При малых скоростях имеем, разлагая (2.6) по степеням

,

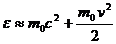т.е. за вычетом энергии покоя, классическое выражение для кинетической энергии. Этот результат не противоречит классической механике, в которой энергия определена с точностью до некоторой аддитивной постоянной.

Подчеркиваем, что полученные формулы в равной степени применимы к любому сложному телу, состоящему из многих частиц, причем под 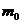надо понимать полную массу тела, а под 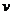- скорость его движения как целого. В четности, формула (2.7) справедлива и для (2.9) покоящегося как целое тело.

Энергия покоящегося тела содержит в себе, наличии энергий покоя входящих в его состав частиц, также и кинетическую энергию частиц и энергию их взаимодействия друг с другом. Другими словами, не равно 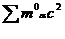( 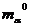- массы частицы), а поэтому . Таким образом, в релятивистской механике не имеет места закон сохранения массы: масса сложного тела не равная сумме масс его частей. Вместо этого имеет место закон сохранения энергии, в которую включается также и энергия покоя частиц. Возводя (2.3) и (2.6) в квадрат и сравнивая их найдем следующее соотношение между энергией и импульсом частицы

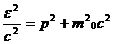(2.8)

Самом деле, имеем

Выразим 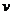через из (*): 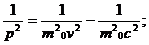отсюда

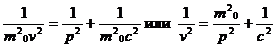подставим в (**)

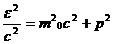
Энергия, выраженная через импульс, называется, как известно, функцией Гамильтона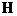

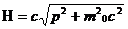(2.9)

При малых скоростях и

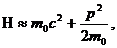(2.9’)

Т.е. за вычетом энергии покоя, получаем известное классическое выражение функцией Гамильтона.

Из выражений (2.3) и (2.6) вытекает также содержащее соотношение между энергией, импульсом и скоростью свободной частицы

(2.10)

При 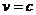импульс и энергия частицы обращаются в бесконечность. Это значит, что частица отличной от нуля массой 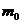не может двигаться со скоростью света. В релятивисткой механике, напротив, могут существовать частицы с массой, равной нулю, движущиеся со скоростью света. Из (2.10) мы имеем для таких частиц

(2.11)

Приближенна эта формула справедлива и для частиц с конечной массой в так называемое ультрарелятивистском случае, когда энергия частицы велика по сравнению с ее энергией покоя

Выведем теперь все полученное соотношение в четырехмерном виде. Согласно принципу наименьшего действия.

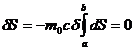
Здесь

= ,

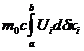Т.к. 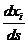есть компонента четырех скорости. Интегрируя по частям, находим

(2.12)

Как известно, для нахождения уравнений движений сравниваются различные траектории, проходящие через два заданных положения, т.е. на пределах 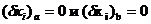. Истинная траектория определяется тогда из условия 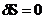. Из (2.12) мы получим бы тогда уравнения , т.е. постоянство скорости свободной частицы в четырех мерном виде.

Запишем уравнение движения нашей свободной частицы в форме Гамильтона – Якоби. Вместе с тем найдем выражение для 4-импульса и связанных с ним величин.

Как известно из механики, уравнение Гамильтона-Якоби определяет производящую функцию, которая, как известно, является действием S, как функции координат. (). Знание действия S, как функцию координат, позволяет найти импульс и полностью решить задачу о движении частицы.

Нас интересует вариация действия как функция координат. Чтобы ее найти будем считать заданной лишь одну точку а, так что 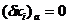. Вторую же точку надо считать переменной, но при этом надо рассматривать только истинные, т.е. удовлетворяющие уравнениям движения траектории. Поэтому в (2.12) интеграл равен нулю. Вместо пишем просто 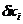и таким образом находим

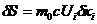(2.13)

В соответствии с механикой в нашем случае 4-вектор с составляющими 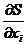называется 4-импульсом. Мы будем обозначать его посредством . Из (2.13) видно, что компоненты 4- импульса для свободной материальной частицы равна

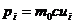(2.14)

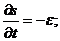Из механики известно, что есть три компоненты импульса частицы, а производная есть энергия частицы (в механике – в случае, когда гамильтониан от явно не зависит, в нашем случае свободной частицы – это само собой разумеется). Пользуясь (1.42), действительно находим в соответствии с (2.14)

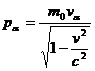сравни с (2.3) (2.15)

Помимо того

Итак, в релятивистской механике импульс и энергия является компонентами одного 4- вектора. Отсюда непосредственно вытекают формулы преобразования импульса и энергии при переходя от одной и.с.о. к другой. Именно подставляя в общие формулы (1.27) преобразования 4- вектора выражения (2.15), находим

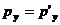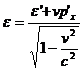, , , (2.16)

По аналогии с обычным определенная силы определим 4- вектор силы как производную

(2.17)

Поскольку 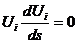, то такому же тождеству

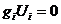(2.18)

удовлетворяют и компоненты 4-силы. Пространственные и временные компоненты этого 4-вектора связаны с обычным трех мерным вектором силы 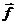соотношениями

(2.19)

В самом деле

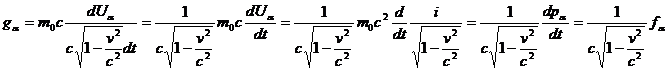
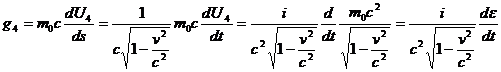
Но , поэтому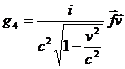

Из определения (2.14) 4-импульса и 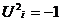имеем

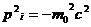(2.20)

Подставляя сюда выражение (2.15) для компонент , мы вернемся к соотношению (2.8).

Подставляя в (2.20) вместо 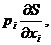находим

(2.21)

или, если написать сумму в явном виде:

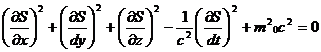(2.22)

это и есть уравнение Гамильтона для свободной релятивистской частицы.

Для перехода к предельному случаю классической механики учтем, что в классической механике энергия не содержит члена , его в (2.9’) Поскольку , то при переходе к классической механике надо вместо S ввести новое действие 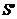согласно соотношению

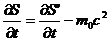
отсюда

, где 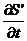очевидно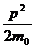

Тогда имеем (2.9’)

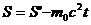
Подставляя его в (2.22), находим

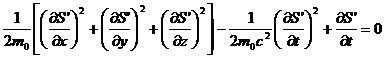
В пределе при 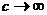имеем классическое уравнение Гамильтона для свободной частицы.

В заключении остановимся понятии массы в релятивистской механике. В вышеприведенных соотношениях фигурирует масса 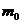частицы. Во все эти соотношения эта масса входит как инвариантная величина, величина одинаковая во всех и.с.о. Между тем же уравнение (2.3) для импульса мы можем также записать и в привычной форме:

если считать, что величина m, связана с инвариантной массой 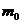соотношением

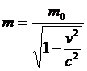(2.23)

Это соотношение показывает, что вновь введенная масса зависит от скорости частицы, при этом она возрастает со скоростью. При малых скоростях она равна массе 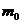, которую мы будем называть теперь массой покоя.

Гл III. Релятивистская электродинамика.

Не нашли, что искали? Воспользуйтесь поиском: