Преобразования Лоренца для поля.

Найдем формулы преобразования для поля, т.е формулы, по которым можно определить поле в одной и.с.о., зная поле в другой.

Формулы для потенциалов находятся непосредственно из общих формул преобразования 4-вектора (1.27)

Тогда

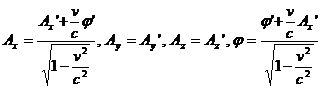(3.34)

Формулы преобразованная для компонент тензора можно было бы найти по общей формуле преобразования 4-тензоров (1.27) Проще однако поступить следующим образом. Вспомним, что переход от системы отсчета к системе , движущейся вдоль оси X, эквивалентен поводу в 4-х мерном пространстве в плоскости . Компоненты же тензора преобразуются как произведения двух составляющих координат. Координаты и при этом преобразовании не меняются. Поэтому

(3.35)

Далее, поскольку координаты y и z не меняется, компоненты преобразуются соответственно как координаты . Согласно (1.25), находим

(3.36)

Вращения системы координат в плоскости можно также рассматривать как вращение двухмерной системы координат в двухмерном же пространстве. Тензор с составляющими 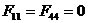, , можно рассмотреть как тензор 2-го ранга в двумерном пространстве , но если антисимметричный тензор имеет ранг, равный числу измерений пространства, то он остается инвариантным при вращении системы координат в этом пространстве. Поэтому при вращении в плоскости

(3.37)

Подставим теперь в (3.35) – (3.37) вместо их вращения через компоненты и согласно (3.28). Мы находим для электрического поля

, (3.38)

И для магнитного поля

, , (3.39)

Таким образом, электрическое и магнитное поле, как большинство физических величин, относительно, т.е. их свойства различны в разных системах отсчетах. В частности электрическое и магнитное поле может быть равно нулю в одной системе отсчета и в тоже время присутствовать в другой системе.

При имеем

,

, ,

Или в векторной форме

(3.40)

Формулы обратного преобразования от к получаются непосредственно из (3.38)-(3.40) перестановкой штриха и изменением знака у V.

Если в системе , то согласно (3.38), (3.39) в системе

(3.41)

Если же в , то в системе

(3.42)

В обоих случаях, в системе магнитное поле и электрическое поле взаимно перпендикулярны.

Наоборот, если в некоторой системе K поля и взаимно перпендикулярны, то существует такая система , в которой поля чисто электрическое или чисто магнитное. Скорость этой системы (по отношению к K) перпендикулярна и и по величине равна в первом случае (причем должно быть ), а во втором (причем ).

Глава IV. Постоянное электромагнитное поле.

Не нашли, что искали? Воспользуйтесь поиском: