Квазистационарное движение зарядов. Постоянное магнитное поле.

В §1-4 мы рассмотрели случаи, когда электрические заряды неподвижны. Рассмотрим теперь случай так называемого квазистационарного движения зарядов. Что понимается под «квазистационарным движением зарядов»?

Пусть заряды совершают финитное движение. В этом случаи они всегда остаются в конечной области пространства. В этой области заряды могут двигаться периодическим или непериодическим образом. В последнем случае, однако, за весьма большое время частицы неизбежно будут проходить если не через те же самые последовательности состояний, как при периодическом движении, то во всяком случае через последовательности близких состояний. Иными словами движение будет почти периодическим, так что можно ввести время Т – характерный период движения.

Будем далее полагать, что движение зарядов системы медленное, а именно скорости зарядов по абсолютной величине много меньше скорости света с. В связи с этим можно пренебречь конечностью скорости распространения электромагнитных полей, так что приближенно поле в каждый момент определяется мгновенным расположением зарядов.

Это и есть условие почти стационарного (квазистационарного) движения зарядов. В этих условиях величины полей и являются конечными и помимо того колеблющимися около некоторых средних значений.

Поэтому представляет интерес рассмотреть среднее по времени магнитное поле , создаваемое зарядами; это поле уже будет функцией координат, но не времени, т. е. будет постоянным. Для определения этого поля усредним по времени уравнение Максвелла

При усреднении воспользуемся формулами:

(4.39)

и

(4.40)

f – конечная функция.

Мы видим, что при периодическом движении , т. к. , а при почти периодическом движении в связи с тем, что характерный период Т весьма большой, а мал можно считать

Усреднение, таким образом, дает

(4.41)   (4.42)

Эти два уравнения и определяют постоянное поле .

Введем средний векторный потенциал согласно

Подставим это в уравнение (4.42), получим

Но мы знаем, что векторный потенциал определен неоднозначно (см. § 3 Гл.III) и поэтому на него можно наложить одно дополнительное условие. Поэтому выберем таким образом, чтобы

(4.43)

Тогда имеем следующее уравнение для определения :

(4.44)

Решение этого уравнения легко найти, если сравнить (4.44) с уравнением Пуассона (4.4). По аналогии с решением (4.10) уравнение Пуассона (4.4) имеем

(4.45)

где R - расстояние от точки наблюдения до элемента dV.

Перейдем в (4.45) от интегрирования к сумме по зарядам. Для этого вместо запишем . Т. к. заряды точечные, то воспользуемся выражением (3.65) для . Тогда вместо интеграла имеем . Далее заметим, что R в (4.45) является переменной интегрирования и потому, конечно, не подвергается усреднению. Поэтому окончательно вместо (4.45) можно написать

(4.46)

Зная можно найти :

(4.47)

Операция rot производится по координатам точки наблюдения. Поэтому rot можно ввести под знак интеграла и при дифференцировании считать постоянным. Применяя известную формулу

где f и любые скаляр и вектор, находим

и следовательно

(4.48)

( направлен из dV в точку наблюдения). Это есть закон Био и Савара.

Магнитный момент.

Рассмотрим среднее магнитное поле, создаваемое системой квазистационарно движущихся зарядов на больших расстояниях от этой системы.

Введем систему координат с началом где-нибудь внутри системы зарядов. Обозначим радиусы-векторы отдельных зарядов посредством , а радиус-вектор точки, в которой мы ищем поле, посредством 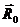. Тогда есть радиус-вектор от заряда до точки наблюдения. Согласно (4.46) имеем для векторного потенциала

(4.49)

Как и в §3 разложим это выражение по степеням с точностью до членов первого порядка (индекс а для кратности опускаем):

В первом члене можно написать

Но среднее значение производной от меняющейся в конечном интервале величины равно нулю (см. (4.40)). Таким образом,

Преобразуем это выражение. Замечая, что , и помня, что 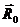постоянный вектор (он не зависит от t), можем написать

Подставим это выражение в . При усреднении производной получим опять нуль, и тогда

Введем вектор

(4.50)

Называемый магнитным моментом системы. Тогда

Найдем напряженность магнитного поля. Имеет

Используя это, получим (помним, что rot,берется по координате ).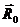

Далее

Таким образом,

(4.51)

или

(4.51’)

где 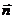- единичный вектор в направлении 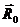. Мы видим, что магнитное поле выражается через магнитный момент такой же формулой, как электрическое поле – через дипольный момент.

Если у всех зарядов отношение заряда к массе одинаково, то мы можем написать

Если , то есть импульс 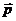заряда и мы получаем

где есть механический момент импульса системы. Таким образом, отношение магнитного момента к механическому в классической электродинамике равно .

Глава V. Электромагнитное поле в вакууме.

Не нашли, что искали? Воспользуйтесь поиском: