Электростатическое поле в диэлектриках.

Основное свойство диэлектриков заключается в невозможности протекания в поле постоянного тока.

Далее мы рассмотрим однородный и изотропный диэлектрик с линейным материальным уравнением

,

(3.1)

Уравнения электростатики при наличии диэлектрика

Граничные условия

при

Здесь напряженность поля, имеющегося в пространстве, в которое внесен диэлектрик и которое поляризует диэлектрик. задано. Индексы (1) и (2) обозначают два разных диэлектрика, имеющих общую границу. Под (2) можно понимать вакуум или проводник.

В приведенной запаси уравнений Максвелла и граничных условий не учтено явно, что мы имеем дело именно с диэлектриком. Очевидно, такой учет можно сделать, если принять во внимание, что внутри диэлектрика и на его поверхности свободный заряд равен нулю.

1. Пусть один диэлектрик окружен вторым диэлектриком. Вторая среда может быть и вакуумом. Тогда имеем следующее уравнений Максвелла

(первая среда) (а) (б)

(3.2)

(вторая среда) (а) (б)

(3.3)

означает, что - электрический потенциал.

К этим уравнениям надо записать граничные условия

	(3.4)
	(3.5)

Эти граничные условия для напряженности 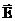эквиваленты граничным условиям для потенциала .

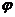	(3.6)
	(3.7)

Сюда же надо приписать условие на бесконечности при .

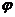. Для потенциала имеет место уравнение Пуассона, если диэлектрик является однородным (). В самом деле, в этом случае из (3.2)(а) следует для первой среды

(3.8)

Аналогичное уравнение имеем для второй среды.

В электродинамике наряду с диэлектрической проницаемостью вводят диэлектрическую восприимчивость æ – коэффициент пропорциональности, входящий в линейную связь дипольного момента с напряженностью. æ . Тогда из , = æ и следует

æ

(3.9)

Можно показать, что æ ≥0. Поэтому ≥1. Для вакуума =1.

Решение рассматриваемой задачи проводят следующим образом: решают уравнения Пуассона для каждой из сред. Т.к. решения в каждой среде неоднозначны, то используют граничные условия (3.6)и(3.7) и при . Основная трудность заключается в использовании граничных условий, так как поверхность раздела двух диэлектриков может быть очень сложной.

2. Пусть вторая среда – проводник. Подобного типа задача (проводник, окруженный диэлектриком) рассматривалась в §6(только там именно проводник был первой средой, а диэлектрик – второй). Поэтому перепишем уравнения для нашей задачи

	в диэлектрике(1-ая среда)	(3.10)
	в проводнике(2-ая среда)

Граничными условиями к этим уравнениям Максвелла

(т.к. )	()
(т.к. )

Первое из этих условий означает постоянство потенциала на поверхности диэлектрика (следующего из эквипотенциальности поверхности проводника).

Сделаем одно физическое замечание как ответ на вопрос, при каких условиях в диэлектрике возникает связанный заряд? В соответствии с (1.17), = æ , (3.9) имеем произвольное

Пусть далее . Тогда и , если диэлектрик неоднородный (т.е. const).

Для однородного диэлектрика при всегда нуль, но это не означает, что (нулю равна ).

В заключении отметим, что, как и в случае 1,решения конкретных задач в случае 2 требуют знания конкретной формы границ.

Не нашли, что искали? Воспользуйтесь поиском: