Тензор электромагнитного поля.

Мы вывели уравнения движения заряда в поле, исходя из функции Лагранжа (3.4), написанной в трехмерном виде. Выведем теперь те же уравнения непосредственно из действия (3.1), написанного в четырехмерных обозначениях.

Принцип наименьшего действия гласит

Учитывая , находим

Первые два члена в подынтегральном выражении проинтегрируем по частям. Кроме того, напишем , где - компоненты 4-скорости.

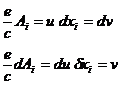
Тогда

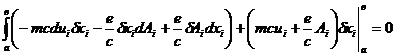(3.23)

Учитывая

Получим

(3.23’)

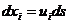Напишем в первом члене во втором и третьем . Кроме того в третьем члене произведем замену . Тогда

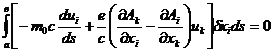
Ввиду произвольности 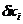, подынтегральное выражение равна нулю, так что

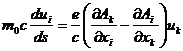(3.24)

Введем обозначение

(3.25)

Тензор называется тензором электромагнитного поля. Уравнение движения (3.24) тогда принимают вид

(3.26)

Эти четыре уравнения и являются уравнениями движения заряда в электромагнитном поле в 4-форме. Из (3.25) следует

(3.27)

- антисимметричен. Учитывая и определение (3.25) находим

из (3.27)

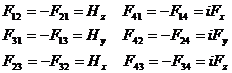
Это можно написать в виде таблицы

(3.28)

Из (3.28) видно, что пространственные компоненты тензора образуют трехмерный антисимметричный тензор 2-го ранга; компоненты этого тензора связаны с магнитным полем. Вектор есть аксиальный вектор.

Компоненты электрического поля является временными компонентами . Векторы есть обычный, полярный вектор.

Переходя к трехмерным обозначениям легко обнаружить, что первые три уравнения тождественны с уравнением движения (3.16), а четвертое – с уравнением (3.18)

Получим уравнение Гамильтона-Якоби в 4-виде. Для этого рассматриваем действие S как функцию координат и в вариации только истинные траектории. Тогда первый член в (3.23) обратиться в нуль. Во втором члене верхний предел считается переменным и мы получим

(3.29)

Отсюда

(3.30)

4-вектор с составляющими есть 4-вектор обобщенного импульса частицы 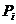. Пользуясь выражениями для 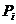и , находим

(3.31)

Как и следовало, пространственные 4-ветора 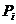образуют трехмерный вектор обобщенного импульса (3.5), а временная есть где полная энергия заряда в поле.

Ввиду того, что 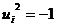, имеем

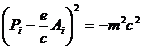, (3.32)

соотношение, совпадающие с (3.7). Заменяя 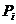на , получим уравнение Гамильтона-Якоби в 4-форме

(3.33)

Не нашли, что искали? Воспользуйтесь поиском: